طباعة الدرس

أسئلة المحتوى وإجاباتها

جمع المتجهات وطرحها

  أتحقق صفحة (23):

ما المقصود بمتجه المحصلة؟

متجه المحصلة: متجه ناتج من الجمع المتجهي لمتجهين أو أكثر.

 

  أتحقق صفحة (24):

ما المقصود بطرح المتجه؟

هو جمع سالب المتجه.

 

  أتحقق صفحة (25):

أوضح المقصود بطريقة المضلع لإيجاد محصلة متجهات عدّة بيانياً.

طريقة المضلع: هي طريقة بيانية لإيجاد محصلة متجهين أو أكثر عن طريق تمثيل المتجهات بأسهم، ثم تركيبها بوضع ذيل المتجه الثاني على رأس المتجه الأول، وهكذا بالترتيب حتى آخر متجه، فيمثل طول السهم الواصل من ذيل المتجه الأول إلى رأس المتجه الأخير مقدار المحصلة، ويمثل اتجاه السهم اتجاه المحصلة.

 

أفكر صفحة (25):

هل يمكن إيجاد الزاوية $\theta$ بطريقة رياضية من دون استخدام المنقلة في المثال 10؟ أوضّح ذلك.

يمكن إيجاد الزاوية $\theta$ بين متجه المحصلة R ومحور -x باستعمال النسب المثلثية؛ سواء كان sin ، أو cos ، أو tan . ففي المثال 10، يمكن حساب الزاوية $\theta$ المبينة في الشكل أدناه على النحو الآتي:

Ɵ = tan^-1$\left|\frac{-1}{-4}\right|$ = tan^-1 0.25 = 14^o

 

أتحقق صفحة (27):

لماذا يعد إيجاد محصلة متجهات عدة بالطريقة التحليلية أكثر دقة من إيجادها بالطريقة البيانية؟

لأن طريقة إيجاد المحصلة بيانيًا تفتقر إلى الدقة، بسبب أخطاء في عمليات القياس؛ وذلك عند قياس الأطوال والزوايا.

 

تمرين صفحة (28):

شحنة كهربائية تؤكر فيها ثلاث قوى كهربائية على النحو الآتي:

200 N في اتجاه الجنوب، 300 N في اتجاه يصنع زاوية مقدارها 53^o شمال الغرب، 500 N في اتجاه الغرب. أجد مقدار محصلة القوى الكهربائية المؤثرة في الشحنة واتجاهها بيانياً.

مقياس الرسم: (1 cm : 100 N)، إذن:

F₃ = 5 cm , F₂ = 3 cm , F₁ = 2 cm

طول سهم المحصلة R هو 6.8 cm ، إذن: مقدار المحصلة R هو:

R = 6.8 cm x $\frac{100 \mathrm{N}}{1 \text{cm}}$ = 680 N

باستعمال المنقلة يتبين أن الزاوية بين متجه المحصلة ومحور +x هي: (176^o).

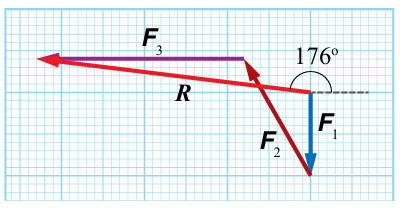
الشكل صفحة (28):

 

  أتحقق صفحة (29):

ما المقصود بتحليل المتجه؟

تحليل المتجهات إلى مركباتها: الاستعاضة عن متجهٍ بمتجهين متعامدين (على محوري x-y مثلاً) يُسميان مركبتي المُتجه، ومحصلتهما المتجه نفسه، وهما يتحدان معه في نقطة البداية.

 

أفكر صفحة (29):

ما علاقة صورة لاعب كرة السلة –في بداية الوحدة- بتحليل المتجهات؟

سدد لاعب كرة السلة نحو المرمى بسرعة محددة v ، وفي اتجاه يصنع زاوية محددة (مثل $\theta$) مع الأفق، فأصبح للسرعة مركبتان:

• مركبة أفقية ($\theta$v cos )، تؤثر في المسافة الأفقية بين الكرة والمرمى.
• مركبة عمودية (v sin $\theta$)، تؤثر في المسافة العمودية بين الكرة والمرمى.

 

تمرين صفحة (30):

أطلقت قذيفة بسرعة v، وكانت المركبة الأفقية للسرعة (-20 m/s) والمركبة العمودية لها (40 m/s). أجد مقدار السرعة v، واتجاهها.

v = $\sqrt{{v_x}^2 + {v_y}^2}$

v = $\sqrt{{(-20)}^2 + {\left(40\right)}^2}$ = 44.7 m/s

يحدد اتجاه السرعة بإيجاد الزاوية التي يصنعها متجه السرعة مع محور (-x):

Ɵ = tan^-1 $\frac{v_y}{v_x}$ = tan^-1 $\left|\frac{40}{-20}\right|$ = tan^-1 (2) = 64^o

 

  أتحقق صفحة (31):

أحدد اتجاه المحصلة عندما تتساوى عندما تتساوى محصلة المركبات على محور +x مع محصلة المركبات على محور +y .

 

أفكر صفحة (31):

إذا كانت محصلة المركبات على محور (R_y) y لمجموعة من المتجهات صفراً، فهل يعني ذلك بالضرورة أن جميع تلك المتجهات تقع فقط على محور x ؟ أفسّر إجابتي.

لا، ليس شرطاً أن تقع تلك المتجهات جميعها على محور  فقط، ولكن يشترط أن يكون مجموع المركبات العمودية الموجبة مساوياً لمجموع المركبات العمودية السالبة (R_y = 0).

 

تمرين صفحة (33):

• أجد مقدار المحصلة واتجاهها في المثال السابق بيانياً، ثمّ أقارن النتائج. ماذا أستنتج؟
• تؤثر ثلاث قوى في نقطة مادية كما في الشكل (31). إذا كات محصلة هذه القوى صفراً. فما مقدار كل من القوتين الأولى والثانية.

مقياس الرسم (1cm : 1u)، والتمثيل البياني موضّح في الشكل التالي:

المحصلة R :

R = 2.3 u , 150^o

 من الملاحظ أن النتائج متقاربة ولكنّ إيجاد المحصلة رياضياً أكثر دقّة منه بيانياً؛ نتيجة الأخطاء في دقة القياس.

المعطيات:

F_1x = 0,     F_2x = 0,   F₃ = 50 N, 330^o

المطلوب:

F₂ = ?,     F₁ = ?

الحل:

المحصلة تساوي صفراً، وهذا يعني أنّ كلاً من محصلة المركبات السينية والمركبات الصادية تساوي صفراً (F_x = 0 , F_y = 0)؛ لذا، فإنّ:

F_x = F_1x + F_2x + F₃ cos (60^o + 270^o)

0 = 0 + F_2x + (50 x 0.87)   F_2x = -43.5 N   F₂ = 43.5 N

F_y = F_1y + F_2y + F₃ sin 330^o

0 = F_1y + 0 + (50 x -0.5) →  F_1y = 25 N →  F₁ = 25 N