طباعة الدرس

إجابات أسئلة مراجعة الوحدة الأولى

المتجهات

السؤال الأول:

أضع دائرة حول رمز الإجابة الصحيحة لكل جملة ممّا يأتي:

1- الكمية المتجهة من الكميات الفيزيائية الآتية، هي:

أ- عدد المسافرين في الطائرة.

ب- المدّة الزمنية لإقلاع الطائرة.

ج- تسارع الطائرة في أثناء إقلاعها.

د- حجم وقود الطائرة.

2- عند جمع القوتين المتعامدتين: 30 N و 20 N جمعاً متجهاً، فإن قيمة القوة المحصلة، هي:

أ- 10 N

ب- 20 N

ج- 50 N

د- 36 N

لأن مقدار المحصلة لا يمكن أن يتجاوز المجموع الجبري للقوتين، ولا يمكن أن يقلّ عن القيمة المطلقة لحاصل طرحهما.

3- ناتج الضرب المتجهي IA x BI في الشكل المجاور هو:

أ- AB sin 90^o

ب- AB sin 30^o

ج- AB cos 30^o

د- AB cos 90^o

4- العلاقة بين متجهي التسارع a₂ ، a₁ بناءً على العلاقة (a₁ – a₂ = 0)، هي:

أ- المتجهان a₂ ، a₁ متساويان في المقدار، ومتعاكسان في الاتجاه.

ب- المتجهان a₂ ، a₁ متساويان في المقدار، وفي الاتجاه نفسه.

ج- المتجهان a₂ ، a₁ مختلفان في المقدار، وفي الاتجاه نفسه.

د- المتجهان a₂ ، a₁ مختلفان في المقدار، ومتعاكسان في الاتجاه.

5- مقدار محصلة القوى واتجاهها في الشكل المجاور، هما:

أ- 30 N باتجاه محور +y

ب- 30 N باتجاه محور -y

ج- 10 N باتجاه محور +y

د- 0 N

6- صوبت سعاد كرة السلة بسرعة مقدارها 20 m/s في الاتجاه المبين في الشكل المجاور. أيّ الآتية تمثل المركبة الأفقية للسرعة:

أ- -20 cos 60^o

ب- 20 cos 60^o

ج- 20 sin 30^o

د- 20 cos 30^o

 

السؤال الثاني:

أحلل: ركل لاعب كرة قدم كتلتها 0.4 kg لتنطلق بسرعة 30 m/s في اتجاه يصنع زاوية مقدارها 37^o مع سطح الأرض الأفقي، وبتسارع مقداره 10 m/s² . استغرقت الكرة مدة زمنية مقدارها 6 s لتعود إلى مستوى سطح الأرض:

أ- أحدد الكميات المتجهة والكميات القياسية.

الكميات المتجهة:

السرعة v ، التسارع a (التسارع ناتج من قوة جذب الأرض للكرة، ويكون اتجاهه عمودياً إلى الأسفل باتجاه مركز الأرض).

الكميات القياسية:

الكتلة m ، الزاوية Ɵ ، الزمن t .

ب- أمثل الكميات المتجهة بيانياً.

تمثل الكميات المتجهة كما في الشكل:

ج- هل يمكن إيجاد محصلة تلك الكميات المتجهة؟ أفسّر إجابتي.

لا؛ لأن الكميات المتجهة مختلف بعضها عن بعض في النوع (السرعة والتسارع).

 

السؤال الثالث:

أحلل: تؤثر قوى عدّة في جسم، كما في الشكل المجاور.

أجد مقدار محصلة القوى المؤثرة في الجسم بالطريقة التحليلية، وأحدد اتجاهها بالنسبة لمحور +x .

F_x = 40 cos 37^o - 10 cos 0 = 22 N

F_y = 40 sin 37^o + 20 sin 90^o - 20 sin 90^o = 24 N

F = R = $\sqrt{F{x}^2 + F{y}^2}$ = $\sqrt{{\left(22\right)}^2 + {\left(24\right)}^2}$ = 32.6 N

$\alpha$ = tan^-1  = $\frac{Fy}{Fx}$ = $\frac{24}{22}$ = 47.5^o

 

السؤال الرابع:

أحسب: متجهان: الأول F = 8 N في اتجاه محور (-y)، والثاني r = 5 m في اتجاه محور (+x). أجد:

أ- 3F

3 F = 3 x 8 = 24 N, -y

ب- -0.5 r

-0.5 r = -0.5 x 5 = 2.5 m, -x

ج- Ir x FI

Ir x FI = 5 x 8 x sin 90^o = 40 m.N , -z

د- Ir x rI

Ir x rI = 5 x 5 x sin 0^o = 0

هـ- F . r

F.r = 8 x 5 x cos 90^o = 0 

 

السؤال الخامس:

حل المشكلات: انطلقت نور من منزلها سيراً على الأقدام، وقطعت مسافة 400 m باتجاه الغرب، ثم اتجهت شمالاً، وقطعت مسافة 200 m لتصل منزل صديقتها. إذا أرادت نور العودة مباشرة إلى منزلها بخط مستقيم، فكم متراً يجب أن تسير؟ في أيّ اتجاه يتعيّن عليها السير حتى تصل منزلها؟

d₂ = 200 m , 90^o  ,  d₁ = 400 m , 180^o

بتمثيل الإزاحتين المقطوعتين، وكي تعود نور إلى منزلها؛ يجب أن تقطع الإزاحة (d)، وبالاتجاه المبين في الشكل الآتي:

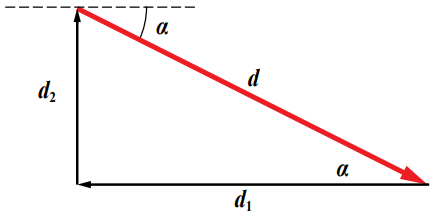
لأنَّ المتجهين متعامدان؛ تُستعمل نظرية فيثاغورس لإيجاد محصلة المتجهين:

d = $\sqrt{{\left(400\right)}^2 + {\left(200\right)}^2}$ = 447 m

α = tan^-1 $\frac{d_2}{d_1}$= tan $\left|\frac{200}{-400}\right|$ = 27^o

 

السؤال السادس:

ثلاثة متجهات للسرعة تشكل مثلثاً مغلقاً، كما في الشكل المجاور. أجد:

أ- v₁ + v₂

v₁ + v₁ = -v₃

v₁ + v₁ = 45 m/s

في اتجاه معاكس لاتجاه المتجه v₃ ، ويمكن استعمال المنقلة لقياس الزاوية بين محور +x والمتجه (v₁ + v₂).

ب- محصلة المتجهات الثلاثة.

المحصلة تساوي صفراً؛ لأنها تُشكل مثلثاً مغلقاً (نقطة البداية تنطبق على نقطة النهاية).

 

السؤال السابع:

أحسب: صوبت سارة كرة تنس أفقياً نحو جدار عمودي، فاصطدمت به بسرعة أفقية v₁ مقدارها 10 m/s باتجاه الشرق، كما في الشكل المجاور، ثم أرتدت عنه أفقياً نحو الغرب بسرعة v₂ مقدارها 7 m/s . أجد التغير في سرعة الكرة (v = v₂ – v₁$∆$).

v₂ = -7 m/s  ,  v₁ = 10m/s

$∆$v = v₂ – v₁ = (-7) – 10 = -17 m/s

 

السؤال الثامن:

أستنتج: ما مقدار الزاوية بين المتجهين: A و B في الحالتين الآتيتين:

أ- IA x BI = A B

A B sin Ɵ = A B

sin Ɵ = 1  →  Ɵ = 90^o

ب- A . B = A B

A B cos Ɵ = A B

cos Ɵ = 1  →  Ɵ = 0^o

 

السؤال التاسع:

أستخدم الطريقة البيانية في حساب ناتج جمع المتجهات وطرحها، كما هو مبين في الشكل الآتي:

ناتج جمع: 2A + B – C + 1.5 D

متجه (E) مقداره (4.1 u)، يقع في الربع الرابع ويميل عن محور (+x) بزاوية (14^o) تقريباً.

محصلة المتجهات: D , C , B , A

متجهة مقداره (5 u) باتجاه المحور (-y).

 

السؤال العاشر:

أحلل: ثلاثة قوارب، كلّ منها يؤثر بقوة في منزل عائم على الماء لسحبه، كما في الشكل المجاور. إذا تحرّك المنزل باتجاه محور (+y)، فأجد:

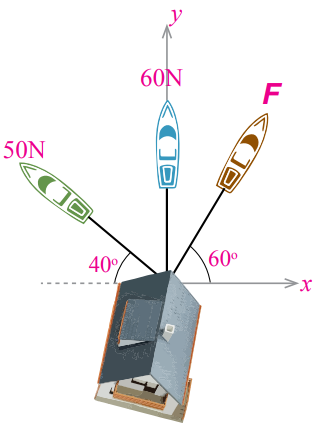
أ- مقدار القوة F .

تحرك المنزل في اتجاه الشمال +y ، وهذا يعني أن اتجاه المحصلة R هو في اتجاه +y أيضاً؛ لذا فإن:

R_x = F cos 60^o + 60 cos 90^o - 50 cos 40^o

0 = 0.5 F + 0 - (50 x 0.76)

F = 76 N

ب- مقدار محصلة القوى الثلاث، محدداً اتجاهها.

R_y = F sin 60^o + 60 sin 90^o + 50 sin 40^o

R = (70 x 0.87) + 60 + (50 x 0.64)

R = 152.9 N

باتجاه الشمال.