طباعة الدرس

إجابات أسئلة مراجعة الدرس

السؤال الأول:

الفكرة الرئيسة: ما مدى صحة الجملة الآتية: كلّ حركة دورية هي حركة تذبذبية، وكلّ حركة تذبذبية هي حركة توافقية بسيطة؟ أدعم إجابتي بأمثلة.

الجملة غير صحيحة، ومثال على ذلك حركة الكزاكب حول الشمس؛ فهي حركة دورية ولكنها ليست تذبذبية ولا توافقية بسيطة، وحركة البندول الذي زاويته أكبر من 15⁰ حركة تذبذبية ولكنها ليست حركة توافقية بسيطة. فالحركة التوافقية البسيطة حالة خاصة من الحركة التذبذبية، والحركة التذبذبية هي حالة خاصة من الحركة الدورية.

 

السؤال الثاني:

أستخدم المتغيرات: بدأ جسم بالتذبذب في حركة توافقية بسيطة من أقصى إزاحة 15 cm ، بحيث يكمل الدورة الواحدة في فترة زمنية مقدارها 3.4 s . أحسب:

أ- التردد.

f = $\frac{1}{T}$ = $\frac{1}{3.4}$ =  0.29 Hz

ب- التردد الزاوي.

= 2πf = 2 x 3.14 x 0.29 = 1.82 rad. s^-1

ج- الإزاحة بعد 3.0 s من بدء الحركة.

x(t) = A cos (t)

x(t) = 0.15 cos (1.82 x 3 rad) = 0.15 cos (5.46 x 57.3⁰)

x(t) = 0.15 cos (312.8⁰) = 0.15 x 0.68 = 0.1 m

 

السؤال الثالث:

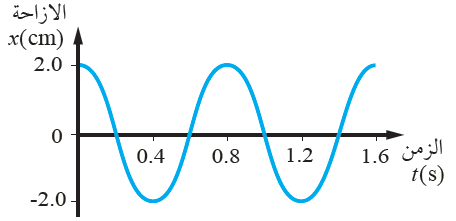أحلل: يتحرك جسم حركة توافقية بسيطة، فإذا بدأ التذبذب من أقصى إزاحة عن موقع اتزانه ومثلت العلاقة بين الإزاحة والزمن بيانياً كما في الشكل، فأجيب عمّا يأتي:

أ- ما مقدار كلّ من السعة والزمن الدوري.

السعة: A = 2 cm = 0.02 m

الزمن الدوري = زمن دورة ذبذبة كاملة = 0.8 s

ب- أكتب معادلة تغير الإزاحة مع الزمن لحركة الجسم.

نحسب أولاً التردد الزاوي:

= $\frac{2\mathrm{\pi }}{T}$ = $\frac{2 x 3.14}{0.8}$ = 7.85 rad/s

معادلة الإزاحة:

x(t) = A cos (t) = 0.02 cos (7.85 t)

 

السؤال الرابع:

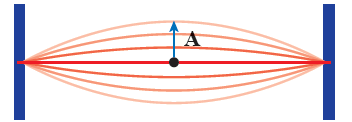أرسم: سُحب وتر آلة موسيقية من نقطة في منتصف إزاحة A كما في الشكل، وتُرك يتذبذب ذهاباً وإياباً في حركة توافقية بسيطة بتردد 5 Hz وسعة 10 mm ، فإذا بدأ التذبذب من أقصى إزاحة عند الزمن (t = 0) من السكون، فأجيب عمّا يأتي:

أ- ما مقدار القيمة العظمى لسرعة النقطة على الوتر.

V_max = A = 2πf A = 2 x 3.14 x 5 x 0.01 = 0.3 m/s

ب- أحسب سرعة النقطة على الوتر عند الزمن (t= 0.12s).

V(t) = - A sin (t)        ,       A = 0.3 $\frac{\mathrm{m}}{\mathrm{s}}$

V(t) = -0.3 sin (2$\mathrm{\pi }$f x t) = -0.3 sin (2 x 3.14 x 5 x 0.12 rad)

= -0.3 sin (3.77 x 57.3⁰) = -0.3 sin (216⁰) = 0.18 m/s

ج- أرسم العلاقة البيانية بين الإزاحة والزمن، وكذلك بين السرعة والزمن.

T = $\frac{1}{f}$ = $\frac{1}{5}$ =  0.2 s

السؤال الخامس:

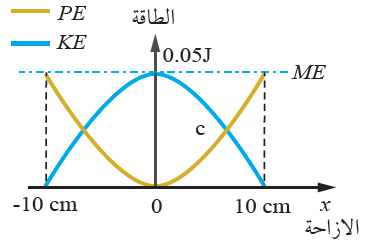التفكير الناقد: يوضّح الشكل المجاور تغيرات كلّ من الطاقة الحركية وطاقة الوضع المرونية، مع الإزاحة لجسم كتلته 400 g يتصل بنابض ويتحرك حركة توافقية بسيطة على سطح أفقي أملس، مستعيناً بالشكل أجيب عمّا يأتي:

أ- أحسب كلاً من ثابت النابض والزمن الدوري.

ثابت النابض k :

PE_max = $\frac{1}{2}$ kA²

0.05 = $\frac{1}{2}$ x k x (0.1)²  $\Rightarrow$  k = $\frac{0.1}{0.01}$ = 10 N/m

الزمن الدوري T :

T = 2π $\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$ = 2 x 3.14 x $\sqrt{\frac{0.4}{10}}$  = 1.26 s

ب- ما مقدار طاقة الوضع المرونية عند موقع الاتزان؟

طاقة الوضع عند موقع الاتزان (x = 0): من الشكل

PE_x=0 = 0 J

ج- أحسب سرعة الجسم لحظة مروره بموقع الاتزان.

سرعة الجسم لحظة مروره بموقع الاتزان (x = 0) تساوي القيمة العظمى للسرعة V_max :

V_max = $\pm$ A = $\pm$ 5 x 0.1 = $\pm$ 0.5 m/s

د- ماذا تمثل نقطة التقاطع c ؟

نقطة التقاطع c هي النقطة التي تتساوى عندها طاقة الوضع مع طاقة الحركة:

PE = KE