اختبار نهاية الوحدة
التكامل
أختار رمز الإجابة الصحيحة في كل مما يأتي:
(1) قيمة هي:
(a
(b
(c
(d
(2) قيمة هي:
0 (a
4 (b
16 (c
8 (d
(3) يبين الشكل الآتي المنطقة المحصورة بين منحنيي الاقترانين: ، في الفترة [1,2-]
التكامل المحدود الذي يمكن عن طريقه إيجاد مساحة المنطقة المظللة هو:
(a
(b
(c
(d
(4) حل المعادلة التفاضلية: الذي تحققه النقطة (0,1) هو:
(a
(b
(c
(d
أجد كلاً من التكاملات الآتية:
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)
(27)
(28)
(29)
(30)
(31)
أجد قيمة كل من التكاملات الآتية:
(32)
(33)
(34)
(35)
(36)
(37)
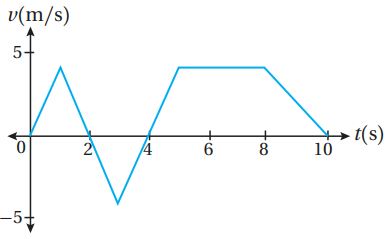 يبين الشكل الآتي منحنى السرعة المتجهة – الزمن لجسيم يتحرك على المحـور x في الفترة الزمنية [0,10]، إذا بدأ الجسيم الحركة من 0=x عندما 0=t، فأجيب عن الأسئلة الثلاثة التالية تباعاً:
يبين الشكل الآتي منحنى السرعة المتجهة – الزمن لجسيم يتحرك على المحـور x في الفترة الزمنية [0,10]، إذا بدأ الجسيم الحركة من 0=x عندما 0=t، فأجيب عن الأسئلة الثلاثة التالية تباعاً:
(38) أجد إزاحة الجسيم في الفترة الزمنية المعطاة.
(39) أجد المسافة التي قطعها الجسيم في الفترة الزمنية المعطاة له.
(40) أجد الموقع النهائي للجسيم.
(41) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين: .
(42) أجد المساحة المحصورة بين منحنيي الاقترانين: .
(43) أجد مساحة المنطقة المحصورة بين منحني الاقترانين: ، والمستقيمين x=2,x=-2
هذه المعادلة التربيعية لا حلول لها، لأن المميز سالب، إذن، منحنيا الاقترانين لا يتقاطعان.
(44) أثبت أن: .
يتحرك جسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: ، حيـث t الزمن بالثواني، وv سرعته المتجهة بالمتر لكل ثانية:
(45) أجد إزاحة الجسيم في الفترة [1,10].
(46) أجد المسافة الكلية التـي قطعها الجسيم في الفترة [1,10].
لتكن d المسافة المقطوعة وهي تمثل المساحة بين منحني والمحور t بين المستقيمين t=1,t=10
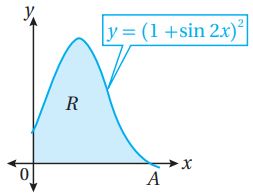 يمثل الشكل المجاور منحنى الاقتران: حيث: :
يمثل الشكل المجاور منحنى الاقتران: حيث: :
(47) أجد إحداثيي النقطة A.
(48) أجد مساحة المنطقة R.
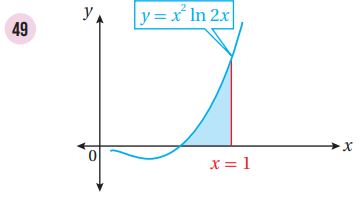
أجد مساحة المنطقة المظللة في كل من التمثيلين البيانيين الآتيين:
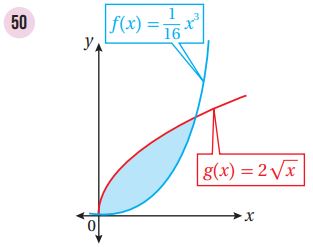
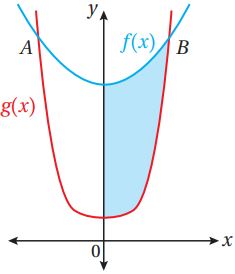 يبين الشكل الآتي منحنيي الاقترانين: :
يبين الشكل الآتي منحنيي الاقترانين: :
(51) إذا كان منحنيا الاقترانين يتقاطعان في النقطة A والنقطة B، فأجد إحداثي نقطتي التقاطع.
(52) أجد حجم المجسّم الناتج من دورات المنطقة المظللة حول المحور x.
نلاحظ أن منحنيي f,g واقعان فوق المحور x، وأن منحنى f فوق منحنى g في الفترة [2,2-]
(53) أجد حجم المجسّم الناتج من دورات المنطقة المحصورة بين منحنى الاقتران: ، والمحور x والمستقيمين: 1=x و 2=x حول المحور x.
أحل كلاً من المعادلات التفاضلية الآتية:
(54)
(55)
(56)
(57)
أجد الحل الخاص الذي يحقق الشرط الأولي المعطى لكل معادلة تفاضلية مما يأتي:
(58)
(59)
أسماك: يتغير عدد الأسماك في إحدى البحيرات بمعدل يمكن نمذجته بالمعادلة التفاضلية: ، حيث x عدد الأسماك، وt الزمن بالسنوات منذ هذه السنة:
(60) أحل المعادلة التفاضلية لإيجاد عدد الأسماك في البحيرة بعد t سنة، علماً بأن عددها هذه السنة هو 300 سمكة.
حيث k ثابت يساوي وبملاحظة أن عدد الأسماك x أكبر من صفر (فيكون )
(61) أجد عدد الأسماك في البحيرة بعد 5 سنوات.
إذن، عدد الأسماك في البحيرة بعد 5 سنوات هو 815 سمكة تقريباً.
(62) تجارة: يمثل الاقتران (p(x سعر القطعة الواحدة (بالدينار) من منتج معين، حيث x عدد القطع المبيعة من المنتج بالمئات. إذا كان: هو معدل التغير في سعر القطعة الواحدة من المنتج، فأجد (p(x، علماً بأن سعر القطعة الواحدة هو 75JD عندما يكون عدد القطع المبيعة من المنتج 400 قطعة.





