طباعة الدرس

أتدرب وأحل المسائل

المتتاليات والمتسلسلات

أكتب كل متسلسلة مما يأتي باستعمال رمز المجموع:

(1) 1 + 4 + 9 + … + 100

$\sum _{k=1}^{10} k^2$

(2) 2 + 4 + 6 + … + 20

$\sum _{k=1}^{10}2 k^{}$

(3) $\frac{1}{2}$ + $\frac{2}{3}$ + $\frac{3}{4}$ + … + $\frac{13}{14}$

$\sum _{k=1}^{13}\frac{ k}{ k + 1}$

(4) -$\frac{2}{3}$ + $\frac{4}{9}$ - $\frac{8}{27}$ + … + $\frac{64}{729}$

$\sum _{k=1}^6 {\left(\frac{-2}{3}\right)}^k$

أجد مجموع كل متسلسلة مما يأتي:

(5) $\sum _{n=1}^6{(-2)}^n$ = 42

(6) $\sum _{n=1}^4\frac{n^2 + 1}{n + 1}$ = $\frac{257}{30}$

(7) $\sum _{n=1}^2\frac{1}{3^n + 1}$= $\frac{7}{20}$

(8) $\sum _{k=1}^6\frac{k^2}{2}$= $\frac{91}{2}$

(9) $\sum _{k=1}^9(12k - 24)$ = 324

(10) $\sum _{k=1}^{20}{k}^3 - 1$ = 44080

أُحدّد إذا كانت كل متتالية مما يأتي حسابية أم لا:

(11) 10, 11, 14, 15, 18, 19, …

ليست حسابية.

(12) 12, 6, 0, -6, -12, …

حسابية أساسها -6

(13) 3, 5, 9, 15, 23, …

ليست حسابية.

أجد الحد العام لكل متتالية حسابية مما يأتي، ثم أجد الحد الثلاثين منها:

(14) 25, 58, 91, 124, …

a_n = 33n – 8

a30 = 982

(15) -1, -$\frac{1}{3}$, $\frac{1}{3}$, 1, …

a_n = $\frac{2}{3}$n – $\frac{5}{3}$

a₃₀ = $\frac{55}{3}$

(16) a₁₇ = -5, d = -$\frac{1}{2}$

a_n = -$\frac{1}{2}$n + $\frac{7}{2}$

a₃₀ = -$\frac{23}{2}$

(17) a₅ = 58, a₁₂ = 30

a_n = 78 – 4n

a₃₀ = -42

أجد مجموع المتسلسلات الحسابية الآتية:

(18) 1 + 5 + 9 + … + 401

401 = 1 + 4(n – 1)  $\Rightarrow$  n = 101

S₁₀₁ = $\frac{101}{2}$(1 + 401) = 20301

(19) 0.7 + 2.7 + 4.7 + … + 56.7

56.7 = 0.7 + 2(n – 1)  $\Rightarrow$  n = 29

S₂₉ = $\frac{29}{2}$(0.7 + 56.7) = 832.3

(20) $\sum _{n=1}^{80}(2n - 2)$

a₁ = 0 , a₈₀ = 158

S₈₀ = $\frac{80}{2}$(0 + 158) = 6320

21) رياضة: يمارس هيثم تمارين الضغط بانتظام، وقد استطاع أداء 25 ضغطة بصورة مستمرة في الأسبوع الأول، ثم تمكن من زيادة عددها أسبوعيًا بمقدار 5 ضغطات على نحو مستمر. ما عدد الضغطات التي يُمكنه أداؤها بشكل مستمر في الأسبوع السادس عشر؟

a₁ = 25 , d = 5

a₁₆ = 25 + 5(15) = 100

22) متسلسلة حسابية منتهية، حدها الأول 10، وأساسها 4، ومجموع حدودها 792، ما عدد حدود هذه المتسلسلة؟

792 = $\frac{n}{2}$(2(10) + (n – 1) x 4)  $\Rightarrow$  2n² + 8n – 792 = 0

      $\Rightarrow$ n² + 4n – 396 = 0

      $\Rightarrow$ (n – 18)(n + 22) = 0

      $\Rightarrow$ n = 18

23) إذا كان مجموع أول n حداً من حدود متسلسلة حسابية هو n² + 4n، فأجد حدها المئة.

S_n = n² + 4n

S₁ = 5  $\Rightarrow$  a₁ = 5

S₂ = 12  $\Rightarrow$  a₂ = 12 – 5 = 7

d = 7 – 5 = 2

a_n = 2n + 3

a₁₀₀ = 203

يبين الشكل المجاور نمطًا هندسياً يمثل عدد النقاط في نماذجه متتالية:

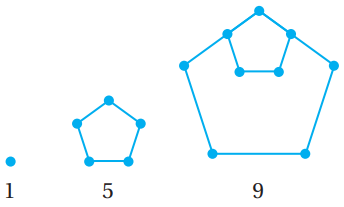
24) أبين أن عدد النقاط في النماذج يمثل متتالية حسابية.

1, 5, 9

ألاحظ أن الفرق بين كل حدين متتابعين، ثابت، وأنه يساوي 4؛ أي إن المتتالية حسابية أساسها 4

25) أجد الحد العام للمتتالية الحسابية.

a_n = 4n - 3

26) هل يوجد نموذج يحوي 397 نقطة؟ أبرر إجابتي.

397 = 4n – 3  $\Rightarrow$  n = 100

بما أن n عدد صحيح موجب، إذن يوجد نموذج يحوي 397 نقطة.

متسلسلة حسابية، حدها الأول a، وأساسها d، ومجموع حدودها الثلاثين الأولى يساوي ضعف مجموع حدودها العشرين الأولى:

27) أثبت أن $\frac{11d}{2}$ = a

S₃₀ = 2S₂₀  $\Rightarrow$  $\frac{30}{2}$(2 + 29d) = 2 x $\frac{20}{2}$(2a + 19d)

      $\Rightarrow$ 20a + 435d = 40a + 380d

      $\Rightarrow$ 10a = 55d

      $\Rightarrow$ a = $\frac{11}{2}$d

28) إذا كان مجموع الحدود الثلاثين الأولى هو 400، فأجد قيمتي a و d.

400 = $\frac{30}{2}$(2a + 29 x $\frac{2}{11}$a)  $\Rightarrow$ a = $\frac{11}{3}$, d = $\frac{2}{3}$

29) أحل المسألة الواردة في بند (مسألة اليوم).

a₁ = 1

a₂ = 1 + 6

a₃ = 1 + 6 + 12

a₄ = 1 + 6 + 12 + 18

…

S₁₀ = 1 + $\frac{9}{2}$(6 + 54) = 271