طباعة الدرس

أتدرب وأحل المسائل

معادلة الدائرية

إجابات دليل المعلم

أكتب معادلة الدائرة في كل من الحالات الآتية:

(1) المركز هو نقطة الأصل، وطول نصف قطرها 7 وحدات.

x² + y² = 49

(2) المركز هو النقطة (3, 1-) ، وطول نصف قطرها 5 وحدات.

(x + 1)² + (y – 3)² = 25

(3) المركز هو النقطة (-3, -2)، وطول قطرها 10 وحدات.

(x + 3)² + (y + 2)² = 25

 

أجد معادلة الدائرة المعطى مركزها وإحداثياً نقطة تمر بها في كل مما يأتي:

(4) المركز (-1, 2)، وتمر بالنقطة (3, 5).

(x + 1)² + (y - 2)² = 25

(5) المركز نقطه الأصل، وتمر بالنقطة (-9, -4).

x² + y² = 97

 

أجد إحداثيي المركز، وطول نصف القطر لكل من الدوائر الآتية:

(6) (x + 5)² + (y – 8)² = 36

r = 6 , (-5, 8)

(7) (x - 19)² + (y – 33)² = 400

r = 20 , (19, 33)

(8) x² + (y + 4)² = 45

r = 3$\sqrt{5}$ , (0, -4)

(9) (x - 3)² + (y + 10)² = 28

r = 2$\sqrt{7}$ , (3, -10)

 

أجد إحداثيي المركز، وطول نصف القطر لكل من الدوائر الآتية:

(10) x² + y² – 6x – 10y + 30 = 0

 (3, 5) , r = 2

(11) x² + y² + 8x = 9

 (-4, 5) , r = 5

(12) 2x² + 2y² + 20x + 36y + 158 = 0

 (-5, -9) , r = 3$\sqrt{3}$

(13) x² + y² - 18x + 14y = 14

 (9, -7) , r = 12

 

أكتب معادلة الدائرة بالصورتين:

 x² + y² + 2fx + 2gy + c = 0 , (x – a)² + (y – b)² = r² ،

حيث: f، وg  ، و c أعداد صحيحة في الحالات الآتية:

(14) المركز (-11, -1)، وطول القطر 26 وحدة.

(x + 11)² + (y + 1)² = 169

x² + y² + 22x + 2y – 47 = 0

(15) المركز (3, 0)، وطول نصف القطر 4$\sqrt{3}$ وحدات.

(x - 3)² + y² = 48

x² + y² - 6x – 39 = 0

(16) المركز (-4, 7)، وتمر بالنقطة (1, 3) .

(x + 4)² + (y - 7)² = 41

x² + y² + 8x - 14y + 24 = 0

 

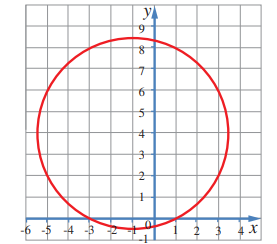(17) أجد معادلة الدائرة المبينة في الرسم البياني المجاور.

مركز هذه الدائرة هو (-1, 4)، ومن الملاحظ أنها تمر بالنقطة (1, 0)؛ لذا، فإن مربع طول نصف قطرها:

2² + 4² = 20

إذن، معادلتها هي: (x + 1)² + (y – 4)² = 20

أو: x² + y² + 2x – 8y – 3 = 0

 

(18) أحل المسألة الواردة في بداية الدرس.

معادلة الدائرة التي تمثل حدود المنطقة التي يصلها البث هي:

(x - 7)² + (y - 4)² = 224²

بتعويض إحداثيات النقطة التي تمثل موقع بيت عمر في المعادلة، فإن:

(-75 – 7)² + (95 – 4)² = 224²

42928704 = 50176

وهي عبارة غير صحيحة.

وبما أن الطرف الأيسر أكبر من الطرف الأيمن، فإن بيت عمر يقع خارج المنطقة التي يصلها البث.

 

(19) أجد إحداثيي المركز وطول نصف قطر الدائرة التي معادلتها:

(2x – 4)² + (2y + 6)² = 100

(2(x - 2))² + (2(y + 3))² = 100

4(x - 2)² + 4(y + 3)² = 100

بالقسمة على 4، فإن : (x – 2)² + (y + 3)² = 25 المركز هو (2, -3)، وطول نصف القطر هو 5 وحدات.

 

(20) دائرة معادلتها 96 = x² + y² + px + 6y ، وطول نصف قطرها 11 وحدة، و p عدد ثابت موجب. أجد بعد مركز الدائرة عن نقطة الأصل.

بإكمال المربع، فإن:

(x + $\frac{P}{2}$)² + (y + 3)² = 96 + ($\frac{P}{2}$)² + 9

r² = 96 + ($\frac{P}{2}$)² + 9

11² = 105 + $\frac{P^2}{4}$  $\Rightarrow$  121 – 105 = $\frac{P^2}{4}$  $\Rightarrow$  p² = 64  $\Rightarrow$  p = 8

إذن:

مركز الدائرة: (-4, -3)، وبعده عن نقطة الأصل: $\sqrt{16+9}$ ؛ أي 5 وحدات.

 

تمثل النقطتان (2, 9) D، و (14, -7) E نهايتي قطر لدائرة مركزها C:

(21) أَجد إحداثي المركز C.

C (8, 1)

(22) أَجد طول نصف القطر.

r = 10

(23) أكتب معادلة الدائرة.

(x – 8)² + (y – 1)² = 100

(24) أثبت أن المستقيم 2 - y = 3x هو مماس للدائرة التي معادلتها:

x² + y² + 4x – 24y + 108 = 0

تعويض y = 3x - 2 في معادلة الدائرة فإن:

x² + (3x – 2)² + 4x – 24 (3x – 2) + 108 = 0

x² + 9x² – 12x + 4 + 4x – 72x + 48 + 108 = 0

10x² - 80x + 160 = 0

x² – 8x + 16 = 0

(x – 4)² = 0

x = 4

y = 3(4) – 2 = 10

إذن، هذا المستقيم مماس للدائرة؛ لأنه يقطعها في نقطة واحدة فقط هي (4, 10).

 

(25) رسم مماس من النقطة (8, 5) P للدائرة التي معادلتها:

x² + y² + 8x – 6y - 75 = 0

أَجد طول القطعة المستقيمة التي تصل النقطة P بنقطة التماس.

4$\sqrt{3}$