طباعة الدرس

أسئلة كتاب التمارين

حالات خاصة من التحليل

أحلل كلاً من المقادير الآتية إلى عواملها:

1) a² - 49

(a – 7)(a + 7)

2) 100 - w²

(10 - w)(10 + w)

3) 9y² - 36

(3y – 6)(3y + 6)

4) x² y² - 64

(xy - 8)(xy + 8)

5) r² – 0.36m²

(r – 0.6m)(r + 0.6m)

6) 24c² – 6

6(2c – 1)(2c + 1)

7) 5y³ m – 45ym³

5ym(y – 3m)(y + 3m)

8) w⁴ – k⁴

(w – k)(w + k)(w² + k²)

9) -y² – 144x²

(12x – y)(12x + y)

10) $\frac{1}{16}$y² – $\frac{4}{9}$

($\frac{1}{4}$y – $\frac{2}{3}$)($\frac{1}{4}$y + $\frac{2}{3}$)

11) xb² – x³ + y² b² – y² x²

(b – x)(b + x)(x + y²)

12) (3y + 2)² – (2y + 3)²

5(y – 1)(y + 1)

أحدد ما إذا كانت كل ثلاثية حدود مما يأتي تمثل مربعاً كاملاً أم لا، وإذا كانت تمثله فأحللها:

13) x² + 2x + 100

(x + 10)² مربع كامل

14) x² + 10x + 16

ليس مربعاً كاملاً

15) y² - 16y + 64

(y - 8)² مربع كامل

16) w² + 8w - 16

ليس مربعاً كاملاً

17) 4x² + 12x + 9

(2x + 3)² مربع كامل

18) 25x² + 10x + 1

(5x + 1)² مربع كامل

19) 4 – 4x + x²

(x - 2)² مربع كامل

20) $\frac{1}{4}$w² + 6w + 36

($\frac{1}{2}$w + 6)² مربع كامل

21) x² + $\frac{2}{3}$x + $\frac{1}{9}$

(x + $\frac{1}{3}$)² مربع كامل

(22) تريد إيمان تغطية جدار مربع الشكل بورق الجدران. إذا كانت مساحة الجدار (x² – 8x + 16) متراً مربعاً، فأجد طول الجدار بدلالة x.

(x – 4) متر.

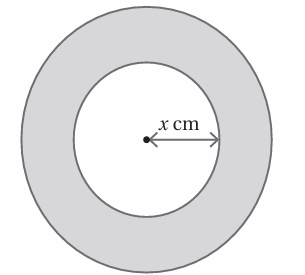في الشكل المجاور قرص رماية مساحت(x² + 6x + 9) π cm² ، أجد:

(23) طول نصف قطر القرص بدلالة x.

(x + 3)

(24) عرض المنطقة المظللة.

3