 |
أتدرب وأحل المسائل
حل المعادلات التربيعية باستخدام القانون العام
أحل كلاً من المعادلات الآتية بالقانون العام، مقرباً إجابتي لأقرب جزء من عشرة (إن لزم):
1) 2x2 + x - 8 = 0
x ≈ 1.8, x ≈ -2.3
2) 3x2 + 5x + 1 = 0
x ≈ -0.2, x ≈ -1.4
3) x2 - x - 10 = 0
x ≈ 3.7, x ≈ -2.7
4) 4x2 + 3 = -9x
x ≈ -0.4, x ≈ -1.8
5) 6x2 + 22x + 19 = 0
x ≈ -1.4, x ≈ -2.3
6) x2 + 3x = 6
x ≈ 1.4, x ≈ -4.4
7) 3x2 + 1 = 7x
x ≈ 2.2, x ≈ 0.2
8) 2x2 + 11x + 4 = 0
x ≈ -0.4, x ≈ -5.1
9) 4x2 + 5x = 3
x ≈ 0.4, x ≈ -1.6
10) 4x2 = 9x - 4
x ≈ 1.6, x ≈ 0.6
11) 7x2 = 2 – 3x
x ≈ 0.4, x ≈ -0.8
12) 5x2 – 10x + 1 = 0
x ≈ 1.9, x ≈ -0.1
أحدد عدد الحلول الحقيقية لكل معادلة تربيعية مما يأتي باستعمال المميز:
13) x2 - 6x + 10 = 0
Δ = -6
لا يوجد حلول حقيقية.
14) 2x2 – 12x = -18
Δ = 0
يوجد حل حقيقي واحد.
15) -5x2 + 8x + 9 = 0
Δ = 244
يوجد حلان حقيقيان مختلفان.
أحل كل معادلة مما يأتي باستعمال أي طريقة، وأبرر سبب اختيار الطريقة:
16) x2 + 4x = 15
إكمال المربع؛ لأن معامل x2 يساوي 1، معامل x زوجي.
= 19, x = -2 (x + 2)2
17) 9x2 - 49 = 0
الجذر التربيعي؛ لأنه على الصورة x2 = d
x = x2 =
18) x2 + 4x – 60 = 0
أستخدم طريقة التحليل لسهولة تحليل الطرف الأيسر.
(x – 6)(x + 10) = 0, x = -10, x = 6
19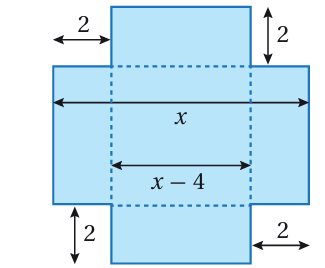
) صناعة: تجري صناعة صندوق معدني من صفيحة مربعة الشكل بقطع 4 مربعات متطابقة من زوايا الصفيحة، طول ضلع كل مربع منها 2m، ثم تطوى الجوانب لتشكيل الصندوق. إذا كان حجم الصندوق 144m3، فأجد أبعاد الصفيحة الأصلية التي صنع منها الصندوق، مقرباً إجابتي لأقرب جزء من عشرة.
x ≈ 12.5 m
20) حديقة: حديقة مستطيلة الشكل يزيد طولها على عرضها بمقدار 5m. إذا كانت مساحتها 60m2، فأجد أبعادها، مقرباً إجابتي لأقرب جزء من مئة.
الطول 10.64 m تقريباً.
العرض 5.64 m تقريباً.
21) هندسة: يبين الشكل الآتي مثلثاً مساحته 10cm2. أجد قيمة x، مقرباً إجابتي لأقرب جزء من عشرة.
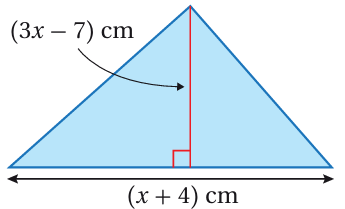
x ≈ 3.3 cm
22) أحل المسألة الواردة في بداية الدرس.
x ≈ 23.2 m