طباعة الدرس

اختبار نهاية الوحدة الثالثة

حل المعادلات

أختار رمز الإجابة الصحيحة لكل مما يأتي:

1) المسافة بين النقطتين A(-1, 4) و B(-3, -2)، هي:

a) $\sqrt{26}$

b) $\sqrt{40}$

c) $\sqrt{20}$

d) $\sqrt{34}$

2) إحداثيا نقطة منتصف $\overline{CD}$؛ حيث C(1, -2) و D(-3, 6)، هما:

a) (-1, 2)

b) (-2, 4)

c) (1.5, -0.5)

d) (-4.5, 1.5)

3) إذا كانت M(-2, -6) نقطة منتصف $\overline{AB}$؛ حيث B(7, 4)، فإن إحداثيي النقطة A هما:

a) (-11, 16)

b) (11, -16)

c) (11, 16)

d) (-11, -16)

4) نقطة تقاطع قطري مربع طول ضلعه s ورأساه (0, 0) و (s, s)، هي:

a) (s, s)

b) (2s, 2s)

c) ($\frac{s}{2}$, $\frac{s}{2}$)

d) ($\frac{s}{2}$, 0)

5) إذا كانت (3, 5), (5, 3), (0, 0) تمثل رؤوس متوازي أضلاع، فإن النقطة التي تمثل الرأس الرابع لمتوازي الأضلاع هي:

a) (5, 0)

b) (3, 0)

c) (2, -2)

d) (2, 2)

أجد المسافة بين كل نقطتين مما يأتي، مقرباً إجابتي لأقرب جزء من عشرة (إن لزم):

6) A(2, 2), B(6, 5)

5 وحدة.

7) N(-3, 2), M(9, 7)

13 وحدة.

8) P(1, 5), T(7, -3)

10 وحدات.

9) F(-6, -4), J(9, 4)

17 وحدة.

أجد إحداثي نقطة منتصف $\overline{AB}$ في كل من الحالات الآتية:

10) A(8, 4), B(12, 2)

(10, 3)

11) A(9, 5), B(8, -6)

(8$\frac{1}{2}$, -1$\frac{1}{2}$)

12) A(-11, -4), B(-9, -2)

(-10, -3)

13) في الشكل الآتي، إذا كانت M نقطة منتصف $\overline{RS}$، فأجد طول $\overline{MR}$ .

MR = 16

14) أجد محيط شبه المنحرف JKLM، المرسوم في المستوى الإحداثي المجاور.

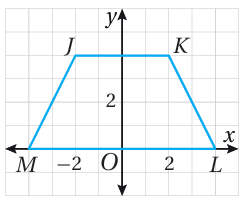
12 + 4$\sqrt{5}$ ≈ 20.9

15) انطلق بلال من منزله إلى المدرسة مروراً بمنزل أشرف. أجد المسافة التي قطعها بلال من منزله إلى المدرسة وأستعين بالمستوى الإحداثي أدناه.

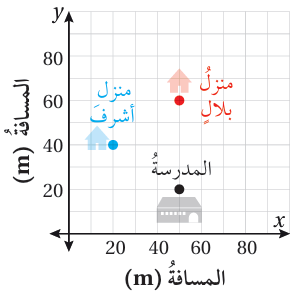
20$\sqrt{13}$ ≈ 72.1 m

أجد البعد بين النقطة والمستقيم في كل مما يأتي

16) y = -x + 2, P(8, 4)

$\frac{10}{\sqrt{2}}$ = 5$\sqrt{2}$ ≈ 7.1

17) x – 3y + 9 = 0, Q =(-13, 6)

$\frac{11\sqrt{10}}{5}$ ≈ 7

18) y – 4x = 7, B(-13, 6)

3$\sqrt{17}$ ≈ 12.4

19) y – 1 = 5x, (3, 3)

$\frac{\sqrt{26}}{2}$ ≈ 2.5

20) y + 2x + 15 = 0, M(-1, -4)

9$\frac{\sqrt{5}}{5}$ ≈ 9

21) 2x + y + 5 = 0, N(0, 0)

$\sqrt{5}$ ≈ 2.3