أتحقق من فهمي

التوزيع الهندسي وتوزيع ذي الحدين

التجربة الاحتمالية الهندسية

أتحقق من فهمي صفحة (164):

أبين إذا كانت التجربة العشوائية تمثل تجربة احتمالية هندسية في كل مما يأتي:

(a) إلقاء عبد العزيز قطعة نقد منتظمة 6 مرات، ثم كتابة عدد مرات ظهور الصورة.

- لدينا ست محاولات مستقلة.

- وفي كل محاولة، يمكن اعتبار ظهور الصورة نجاحاً $(p=\frac{1}{2})$ وظهور الكتابة فشلاً.

- واحتمال النجاح ثابت في كل مرة.

- لكن لا يتم التوقف عند أول نجاح، بل إنه يكمل 6 محاولات مهما كانت النتائج.

لذلك لا تمثل هذه التجربة تجربة احتمالية هندسية.

(b) إطلاق سامية أسهماً بشكل متكرر نحو هدف، ثم التوقف عند إصابته أول مرة، علماً بأن احتمال إصابتها الهدف في كل مرة هو 0.6

- لدينا محاولات مستقلة يتم تكرارها (محاولة إصابة الهدف).

- في كل مرة يمكن اعتبار إصابة الهدف نجاحاً، وعدم إصابته فشلاً.

- احتمال النجاح في كل مرة ثابت وهو $p=0.6$ 

- يتم التوقف عند أول نجاح.

- إذن هذه تجربة احتمالية هندسية لتحقق الشروط الأربعة.

المتغير العشوائي الهندسي وتوزيعه الاحتمالي

أتحقق من فهمي صفحة (166):

يمثل الشكل المجاور قرصاَ مقسـماً إلى 4 قطاعات متطابقة. إذا دلّ المتغير العشوائي X على عدد مرات تدوير مؤشر القرص حتى يقف عند اللون الأخضر أول مرة، فأجد كلاً مما يأتي:

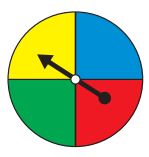
$P(X=3)$ (a)

- لدينا محاولات مستقلة يتم تكرارها (تدوير مؤشر الفرص وملاحظة أين يقف).

- في كل محاولة يمكن اعتبار توقف المؤشر على اللون الأخضر نجاحاً، توقفه عند أي لون غير الأخضر فشلاً.

- احتمال النجاح في كل مرة ثابت وهو $p=\frac{1}{4}$

- يتم التوقف عند أول نجاح.

إذن هذه تجربة احتمالية هندسية لتحقق الشروط الأربعة.

عدد المحاولات للوصول إلى أول نجاح

$X~\mathrm{Geo}\left(\frac{1}{4}\right)\Rightarrow P(X=3)=\left(\frac{1}{4}\right){(1-\frac{1}{4})}^{3-1}=\frac{9}{64}$

$P(X\le 4)$ (b)

$\begin{array}{rl}P(X\le 4)& =P(X=1)+P(X=2)+P(X=3)+P(X=4)\\ & =\left(\frac{1}{4}\right){\left(\frac{3}{4}\right)}^0+\left(\frac{1}{4}\right){\left(\frac{3}{4}\right)}^1+\left(\frac{1}{4}\right){\left(\frac{3}{4}\right)}^2+\left(\frac{1}{4}\right){\left(\frac{3}{4}\right)}^3\\ & =\frac{1}{4}+\frac{3}{16}+\frac{9}{64}+\frac{27}{256}=\frac{175}{256}\approx 0.684\end{array}$

(c) احتمال تدوير مؤشر القرص ثلاث مرات على الأقل حتى يقف عند اللون الأخضر أول مرة.

$\begin{array}{rl}P(X>3)& =1-P(X\le 3)\\ & =1-\left(P\right(X=1)+P(X=2)+P(X=3\left)\right)\\ & =1-(\left(\frac{1}{4}\right){\left(\frac{3}{4}\right)}^0+\left(\frac{1}{4}\right){\left(\frac{3}{4}\right)}^1+\left(\frac{1}{4}\right){\left(\frac{3}{4}\right)}^2)\\ & =1-(\frac{1}{4}+\frac{3}{16}+\frac{9}{64})=1-\frac{37}{64}=\frac{27}{64}\approx 0.422\end{array}$

التوقع للمتغير العشوائي الهندسي 

أتحقق من فهمي صفحة (168):

تسويق: أعلنت إحدى شركات تصنيع حبوب الفطور للأطفال عن وجود لعبة مجانية في بعض علب الحبوب الجديدة التي تنتجها الشركة. إذا احتوت علبة من كل 4 علب على لعبة، ودلّ المتغير العشـوائي X على عدد العلب التي سيفتحها الطفل حتى يجد لعبة، فكم علبة يتوقع أن يفتحها الطفل حتى يجد أول لعبة؟

بما أن الطفل يكرر فتح العلب حتى يصل إلى علبة فيها لعبة، فيمكن اعتبار x عدد المحاولات متغيراً عشوائياً هندسياً، أي:

$X~\mathrm{Geo}\left(\frac{1}{4}\right)\Rightarrow E\left(X\right)=\frac{1}{\frac{1}{4}}=4$

التجربة الاحتمالية ذات الحدين

أتحقق من فهمي صفحة (169):

أبين إذا كانت التجربة العشوائية تُمثل تجربة احتمالية ذات حدين في كل مما يأتي:

(a) إلقاء حجر نرد منتظم 20 مرة، ثم كتابة عدد المرات التي ظهر فيها العدد 1 على الوجه العلوي لحجر النرد.

- يتم تكرار إلقاء حجر النرد وملاحظة العدد الظاهر على الوجه العلوي، وهذه المحاولات مستقلة.

- في كل محاولة يعد (النجاح) ظهور العدد (1) على الوجه العلوي، و(الفشل) ظهور أي عدد غير (1) على الوجه العلوي.

- احتمال النجاح في كل مرة ثابت وهو $p=\frac{1}{6}$

- عدد المحاولات محدد سلفاً وهو 20 محاولة.

إذن، هذه تجربة احتمالية ذات حدين، لتحقق الشروط الأربعة.

(b) اختيار 7 طلبة عشوائياً من صف روضة فيه 15 ولداً و10 بنات، وذلك لتشكيل فريق لإحدى الألعاب، ثم كتابة عدد البنات اللاتي وقع عليهن الاختيار.

محاولات اختيار 7 من طلبة روضة غير مستقلة لأن احتمال اختيار بنت غير ثابت في جميع المحاولات. إذن هذه ليست تجربة احتمالية ذات حدين.

المتغير العشوائي ذو الحدين وتوزيعه الاحتمالي

أتحقق من فهمي صفحة (172):

(a) ألقت عائشة حجر نرد منتظماً 10 مرات. ما احتمال ظهور الرقم 1 على الوجه العلوي 3 مرات فقط.

لدينا تجربة عشوائية ذات حدين، وعدد مرات ظهور الرقم (1) على الوجه العلوي هو متغير عشوائي x ذو حدين، لأن:

لدينا محاولات مستقلة متكررة (إلقاء حجر النرد) حيث (النجاح) هو ظهور الرقم (1) على الوجه العلوي (واحتماله ثابت $p=\frac{1}{6}$)، والفشل ظهور رقم غير (1)، وعدد المحاولات محدد سلفا وهو 10=n

$\begin{array}{rl}& \Rightarrow X~B(10,\frac{1}{6})\\ & P(X=3)=\left(\begin{array}{c}10\\ 3\end{array}\right){\left(\frac{1}{6}\right)}^3{(1-\frac{1}{6})}^{10-3}=\left(\begin{array}{c}10\\ 3\end{array}\right){\left(\frac{1}{6}\right)}^3{\left(\frac{5}{6}\right)}^7\\ & =\frac{10\times 9\times 8}{6}\times \frac{5^7}{6^{10}}\approx 0.155\end{array}$

(b) تحتوي آلة حاسبة على 16 زراً للأعداد من 0 إلى 9، إضافة إلى العمليات الأساسية، والمساواة، والفاصلة العشرية. إذا أغمض أحمد عينيه، ثم ضغط على أزرار هذه الآلة 20 مرة بصورة عشوائية، فما احتمال أن يضغط على أزرار العمليات الحسابية الأساسية 3 مرات فقط؟

التجربة العشوائية المذكورة هي ذات حدين، لأن هناك محاولات مستقلة متكررة (ضغط زر)، والنجاح هو الضغط على أحد أزرار العمليات الحسابية الأساسية، والفشل هو الضغط على زر من باقي الأزرار، احتمال النجاح كل مرة ثابت وهو $p=\frac{4}{16}=\frac{1}{4}$ وعدد المحاولات محدد سلفاً n=10

$\begin{array}{rl}& \Rightarrow X~B(20,\frac{1}{4})\\ & P(X=3)=\left(\begin{array}{c}20\\ 3\end{array}\right){\left(\frac{1}{4}\right)}^3{(1-\frac{1}{4})}^{20-3}=\left(\begin{array}{c}20\\ 3\end{array}\right){\left(\frac{1}{4}\right)}^3{\left(\frac{3}{4}\right)}^{17}\approx 0.134\end{array}$

(c) إذا كان احتمال نجاح عملية جراحية هو 0.8، وأجرى طبيب هذه العملية 10 مرات خلال عام واحد، فما احتمال أن تنجح 7 عمليات منها على الأقل؟

التجربة المذكورة هي عشوائية ذات حدين، لأن لدينا محاولات مستقلة متكررة (إجراء العملية) واحتمال النجاح كل مرة ثابت هو 0.8=p، وعدد المحاولات محدد سلفاً وهو 10=n ليكن x عدد مرات النجاح.

$\begin{array}{rl}& \Rightarrow X~B(10,0.8)\\ & P(X\ge 7)=P(X=7)+P(X=8)+P(X=9)+P(X=10)\\ & =\left(\begin{array}{c}10\\ 7\end{array}\right)\left(0.8{)}^7\right(0.2{)}^3+\left(\begin{array}{c}10\\ 8\end{array}\right)\left(0.8{)}^8\right(0.2{)}^2+\left(\begin{array}{c}10\\ 9\end{array}\right)\left(0.8{)}^9\right(0.2{)}^1+\left(\begin{array}{c}10\\ 10\end{array}\right)\left(0.8{)}^{10}\right(0.2{)}^0\\ & =0.201+0.302+0.268+0.107\approx 0.878\end{array}$

التوقع والتباين للمتغير العشوائي ذي الحدين 

أتحقق من فهمي صفحة (173):

سيارات: بعد إجراء مسح للسيارات التي صنعتها شركة ما، تبين أن في %5 منها عطلاً ميكانيكياً. إذا استورد وكيل للشركة في إحدى الدول 1000 سيارة، فأجد عدد السيارات التي يتوقع أن يظهر فيها هذا العطل.

ليكن x عدد السيارات التي فيها عطل ضمن الألف سيارة، إذن، $X~B(1000,0.05)$

$E\left(X\right)=np=1000\times \frac{5}{100}=50$

إذن، يتوقع أن تكون في هذه الشحنة من السيارات خمسون سيارة بها هذا العطل الميكانيكي. 

التباين للمتغير العشوائي ذي الحدين 

أتحقق من فهمي صفحة (175):

فحص مراقب الجودة في أحد المصانع 500 عينة عشوائياً من الخلطات الخرسانية، فوجد أن 10 منها لا تطابق المواصفات. إذا فحص مراقب الجودة 200 عينة أخرى، فأجد كلاً مما يأتي:

(a) العدد المتوقع من العينات التي لا تطابق المواصفات من العينات العشرين التي فحصها مراقب الجودة.

ليكن x عدد العينات التي لا تطابق المواصفات ضمن الـ 200 عينة التي اختارها المراقب أخيراً.

$\Rightarrow X~B(200,\frac{1}{50})$

حيث اعتمدنا هنا $p=\frac{10}{500}=\frac{1}{50}$ بالاستناد إلى الاحتمال التجريبي لاختيار عينة غير مطابقة الحاصل في 500 عينة الأولى.

$E\left(X\right)=np=200\times \frac{1}{50}=4$

لذا يتوقع وجود 4 عينات لا تطابق المواصفات ضمن هذه العينات الـ200.

(b) تباين عدد العينات التي لا تطابق المواصفات من العينات العشرين التي فحصها مراقب الجودة.

$\mathrm{Var}\left(X\right)=np(1-p)=200\left(\frac{1}{50}\right)\left(\frac{49}{50}\right)=3.92$