إجابات أتحقق من فهمي

نظريتا الباقي والعامل

صفحة (54):

أستعمل طريقة الجدول؛ لأجد ناتج كلّ ممّا يأتي:

a) (x³ + 6x² – 9x – 14) $÷$ (x + 1)

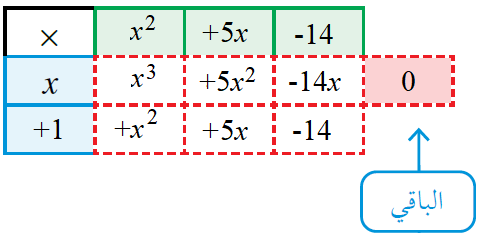
   ناتج القسمة هو x² + 5x - 14 ، والباقي 0     

b) (2x³ - x² + 3) $÷$ (x - 3)

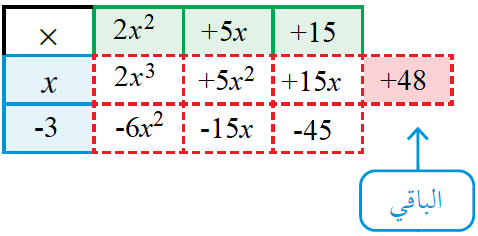
     ناتج القسمة هو x² + 5x + 152 ، والباقي 48     

صفحة (57):

أستعمل نظرية الباقي؛ لأجد باقي قسمة P(x) على h(x) في كلّ ممّا يأتي:

a) $P\left(x\right)=4x^4-7x^3+5x^2+2, h\left(x\right)=x-1$

   $P\left(1\right)=4 \mathrm{هو} \text{الباقي }$ 

b) $P\left(x\right)=3x^3+8x^2-3x-6, h\left(x\right)=x+3$

   $\text{P}(-3)=-6 \mathrm{هو} \text{الباقي }$

c) $P\left(x\right)=-2x^3-5x^2+10x+9, h\left(x\right)=2x+8$

   $P(-\frac{8}{2})=P(-4)=17 \mathrm{هو} \text{الباقي}$

صفحة (58):

إذا كان P(x) = x³ – 2x ² – 13 x - 10

  $\begin{array}{r}\mathrm{a}) P(5)=5^3-2(5{)}^2-13\left(5\right)-10\\ =125-50-65-10=0\end{array}$

$\mathit{\text{P}}\text{(}\mathit{\text{x}}\text{) عوامل من عامل (}\mathit{\text{x}}\text{-5) إذن}$           

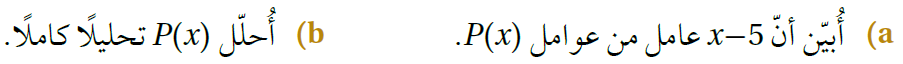
لتحليل P(x) أقسم P(x) على (x - 5)b)      

        P(x) = (x – 5) (x² + 3x + 2)

                = (x – 5) (x + 2) (x + 1)

صفحة (61):

أجد أصفار كثيرات الحدود الآتية جميعها:

a) P(x) = 5x³ – x² – 5x + 1

عوامل الحد الثابت هي: $\pm 1$ ، وعوامل المعامل الرئيس هي $\pm 1$ ، و $\pm 5$ ، الأصفار المحتملة للاقتران هي: $\frac{1}{5}\pm$ ، $\pm 1$
بالتعويض نجد أن P(1) = 5 – 1 – 5 + 1 = 0

إذن: (x-1) هو أحد عوامل P(x)

أجد العوامل الأخرى بالقسمة وتحليل الناتج إن أمكن.

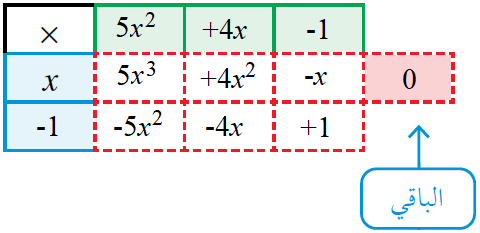
P(x) = (x-1) (5x² + 4x – 1)

        = (x-1) (5x-1) (x+1)

إذن، أصفار P(x) هي: $\frac{1}{5}$ ، -1 ، 1

b) Q(x) = x⁴ + 6x³ + 7x² – 6x - 8

معامل الحد الرئيس يساوي 1 ، فالأصفار المحتملة هي عوامل الحد الثابت 8 ، وهي: $\pm 8$ ، $\pm 4$ ، $\pm 2$ ، $\pm 1$

بالتعويض نجد أنّ: Q(1) = 1 + 6 + 7 – 6 – 8 = 0

إذن: (x-1) هو أحد عوامل Q(x)

أجد العوامل الأخرى بالقسمة وتحليل الناتج إن أمكن.

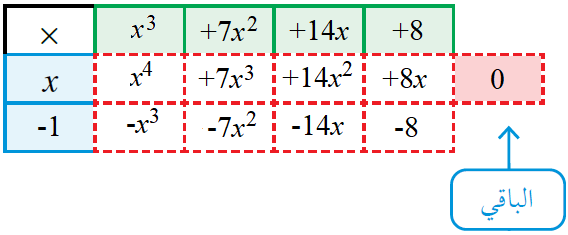
Q(x) = (x-1) (x³ + 7x² + 14x + 8)

وبتعويض x = -1 في العامل التكعيبي نجد أن الناتج 0 ،

نقسم x³ + 7x² + 14x + 8 على (x+1).

فنجد أنّ:

Q(x) = (x-1) (x+1) (x² + 6x + 8)

         = (x-1) (x+1) (x+2) (x+4)

إذن أصفار Q(x) هي: 1- , 1 , -2 , -4

صفحة (63):

أحل كلّ معادلة ممّا يأتي:

a) x³ - x² – 9x + 9 = 0

    x²(x -1) – 9(x -1) = 0

    (x -1) (x ²-9) = 0

    (x -1) (x -3) (x +3) = 0

     x = 1 , x = 3 , x = -3

إذن، حلول هذه المعادلة هي: x = 1 , x = 3 , x = -3

b) x³ + 3x² – 4 = 0

حلول هذه المعادلة هي: x = 1 , x = -2 ،  ويمكن حلها بتحليل الطرف الأيسر إلى عوامل بطريقة مشابهة لحل الفقرة (a)، ويمكن حلها بطريقة المثال (5).

صفحة (64):

يزيد ارتفاع أسطوانة 5 cm على طول نصف قطر قاعدتها. إذا كان حجم الاسطوانة 72π cm³ ؛ فما طول نصف قطر قاعدتها وارتفاعها؟

نصف قطر قاعدة الاسطوانة 3 cm ، وارتفاعها 8 cm