أسئلة المحتوى وإجاباتها
أتحقق صفحة (56):
أفرق بين الموجات المستعرضة والموجات الطولية.
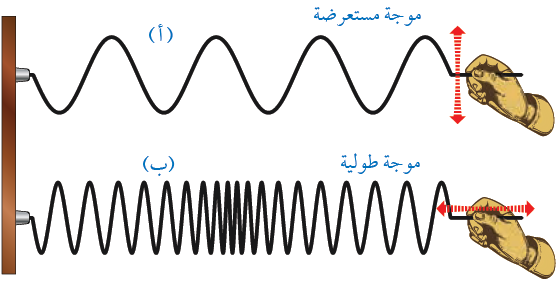
في الموجات الطولية يكون اتجاه اهتزاز أجزاء الوسط باتجاه انتشار الموجة نفسه، وفي الموجات المستعرضة يكون اتجاه اهتزاز أجزاء الوسط متعامد مع اتجاه انتشار الموجة.
الشكل (3) صفحة (58):
مكونات الطيف الكهرمغناطيسي المرئي وغير المرئي.
أستخرج من الشكل تطبيقاً تكنولوجياً واحداً لاستخدام كل من موجات الراديو، وموجات الأشعة تحت الحمراء، وموجات الأشعة السينية، وموجات أشعة جاما.
موجات الراديو: الاتصالات، موجات الأشعة تحت الحمراء: أجهزة الإنذار والتحكم، موجيات الأشعة السينية: تصوير العظام، موجات أشعة جاما: في الطب.
أتحقق صفحة (60):
أوضّح المقصود بكل من التردد والزمن الدوري، ثم أصف العلاقة بينهما.
التردد: عدد الموجات التي تعبر نقطة محددة في الوسط خلال ثانية واحدة.
الطول الموجي: المسافة بين قمتين متتاليتين أو قاعين متتاليين.
العلاقة بينهما عكسية، بزيادة أحدهما تقل الأخرى.
أتحقق صفحة (61):
عن طريق المقارنة بين الشكلين (5/أ) و (5/ب)، أستنتج تماثلاً في الشكل بين الطول الموجي والزمن الدوري. أفسر هذا التماثل.

يمثل الطول الموجي المسافة بين قمتين متتاليتين، علماً أن القمتان تمثلان موقعين في الوسط لهما الإزاحة الرأسية العظمى نفسها، في حين يمثل الزمن الدوري الفاصل الزمني بين قمتين متتاليتين، علماً أن القمتين تمثلان لحظتين زمنيتين تكون فيهما الإزاحة الرأسية للموقع نفسه قيمة عظمى.
أتحقق صفحة (63):
أجد المسافة في الشكل (7) بين كل من (d, e) ونقطة الأصل بدلالة الطول الموجي، ثم أحدد زاوية الطور المقابلة لكل موقع.
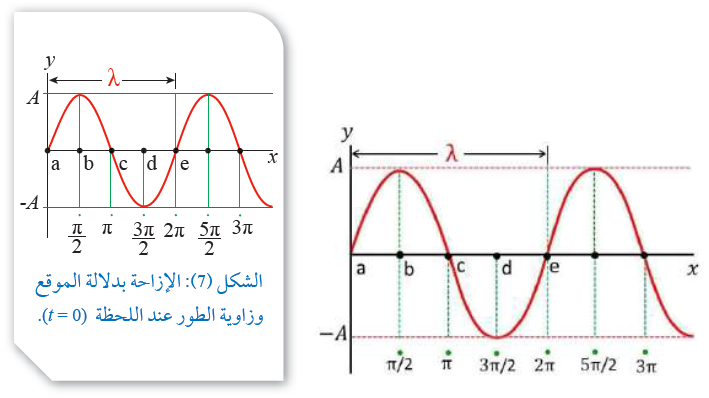
النقطة (e) تبعد عن نقطة الأصل طول موجي واحد.
النقطة (d) تبعد عن نقطة الأصل ثلاثة أرباع الطول الموجي.
فرق الطور بينهما: 2π - =
أتحقق صفحة (68):
ما فرق المسار بين الموجتين، الذي يقابله فرق طور مقداره (π)؟
إذا كان فرق الطور (2π) يقابل موجة واحدة، فإن فرق طور مقداره (π)، يعطي فرق المسار ().
الشكل (12) صفحة (68):
موجتان متساويتان في التردد والطول الموجي، ومختلفتان في طول المسار.
أستخرج من الشكل طول مسار كل موجة وفرق المسار بين الموجتين بدلالة الطول الموجي.
المسار الأول d1 يساوي 6λ
المسار الثاني d2 يساوي λ
فرق المسار d يساوي:
λ - 6λ =
إعداد : شبكة منهاجي التعليمية
20 / 03 / 2022
النقاشات