أتحقق من فهمي
المحل الهندسي في المستوى المركب
الدائرة
أتحقق من فهمي صفحة 169
أجد المحل الهندسي الذي تمثله المعادلة: ، ثم أكتب المعادلة بالصيغة الديكارتية.
وهذه معادلة دائرة في المستوى المركب مركزها (-5, 4)، وطول نصف قطرها 7
وهذه معادلة دائرة مركزها (-5, 4)، وطول نصف قطرها 7
أتحقق من فهمي صفحة 171
إذا كانت: ، فأجيب عن السؤالين الآتيين تباعاً:
(a) أرسم المحل الهندسي الذي تمثله المعادلة في المستوى المركب.
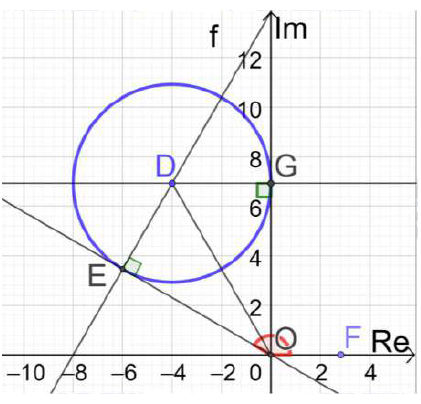
وهذه معادلة دائرة في المستوى المركب مركزها (-4, 4)، وطول نصف قطرها 4
(b) أجد القيمة العظمى لسعة الأعداد المركبة z التي تحقق المعادلة.
أكبر سعة للعدد المركب z تساوي قياس الزاوية FOE المحصورة بين مماس الدائرة OE والمحور الحقيقي الموجب.
مماسا الدائرة OG و OE عموديان على الترتيب على نصفي القطرين DG و DE .
المثلثان OGD و OED متطابقان بثلاثة أضلاع، إذن الزاويتان GOD و EOD متطابقتان.
القيمة العظمى لسعة الأعدد المركبة z التي تحقق المعادلة المعطاة هي:
المنصف العمودي للقطعة المستقيمة
أتحقق من فهمي صفحة 172
أجد المحل الهندسي الذي تمثله المعادلة: ، ثم أكتب المعادلة بالصيغة الديكارتية.
وهذه هي معادلة المنصف العمودي للقطعة المستقيمة الواصلة بين النقطتين (0, 5)، (-1, 0).
إذن معادلة المنصف العمودي للقطعة المستقيمة بالصيغة الديكارتية هي:
x + 5y - 12 = 0
إعداد : شبكة منهاجي التعليمية
19 / 01 / 2023
النقاشات