مهارات التفكير العليا
التوزيع الهندسي وتوزيع ذي الحدين
(38) أكتشف الخطأ: أرادت لانا حل السؤال الآتي:
"عند إلقاء قطعة نقد غير منتظمة، كان احتمال ظهور الصورة هو ، إذا ألقيت قطعة النقد بصورة متكررة حتى تظهر الصورة أول مرة، فما احتمال أن تظهر الصورة أول مرة عند إلقاء قطعة النقد في المرة الثالثة ؟" وكان حلها على النحو الآتي:
أكتشف الخطأ في حل لانا، ثم أصححه، مبرراً إجابتي.
X متغير عشوائي هندسي.
أخطأت لانا في الأس الذي وضعته فوق القوس، فقاعدة حساب احتمال المتغير العشوائي الهندسي تحوي (1-x) في الأس وليس x (أي المفروض أقل من قيمة x بواحد، وليس قيمة x المطلوبة ذاتها).
(39) تحد: ترسل إحدى الشركات استبانة إلكترونية إلى زبائنها بعد بيعهم منتجاً ما؛ لتعرف التغذية الراجعة حيال المنتج. ولضمان ذلك الشركة تكرر إرسال كل استبانة إلى حين رد الزبون. إذا كان احتمال رد الزبون على الاستبانة في المرة الأولى أكبر من 0.5، واحتمال رده على الاستبانة في المرة الثانية عند عدم رده على الاستبانة في المرة الأولى هو 0.21، وبافتراض أن هذه المحاولات مستقلة، فأجد توقع عدد الاستبانات التي سترسلها الشركة إلى حين رد الزبون، علماً بأن احتمال رد الزبون على أي استبانة لا يتأثر بعدد مرات إرسالها.
إذا كان X يدل الرسالة إلى حين الرد عليها لأول مرة، فإن:
لكن احتمال الرد على الاستبانة في المرة الأولى أكبر من 0.5، إذن 0.7=p
تبرير: إذا كان عدد الطلبة في أحد الصفوف 25 طالباً، فأجد كلاً مما يأتي:
(40) احتمال أن يكون طالب واحد فقط من مواليد شهر آذار.
ليكن X عدد الطلبة المولودين في شهر آذار
وذلك لأن احتمال النجاح في كل مرة هو:
(41) احتمال أن يكون 3 طلبة فقط من مواليد شهر آذار.
(42) احتمال أن يكون اثنان من الطلبة فقط من مواليد فصل الشتاء.
ليكن X عدد الطلبة المولودين في فصل الشتاء
حيث p هو احتمال أن أي منهم مولود في فصل الشتاء:
(43) تحد: إذا كان: ، فأجد .
إعداد : شبكة منهاجي التعليمية
17 / 02 / 2023
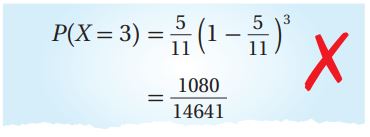
النقاشات