أتدرب وأحل المسائل

التوزيع الطبيعي

إذا اتخذ التمثيل البياني لكتل الطلبة في إحدى المحافظات منحنى طبيعياً، فأجد كلاً مما يأتي:

(1) النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي.

النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي هي %50

وذلك من خواص منحنى التوزيع الطبيعي (تماثل البيانات حول الوسط الحسابي).

(2) النسبة المئوية للطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحراف معياري واحد.

النسبة المئوية للطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحراف معياري واحد هي: 

$\frac{1}{2}\left(68\mathrm{\%}\right)=34\mathrm{\%}$ 

(3) النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي بمقدار لا يقل عن انحرافين معياريين.

النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي بمقدار لا يقل عن الحرافين معياريين هي:

$\frac{1}{2}(100\mathrm{\%}-95\mathrm{\%})=2.5\mathrm{\%}$

(4) النسبة المئوية للطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحرافين معياريين، أو تزيد عليه بمقدار لا يزيد على ثلاثة انحرافات معيارية.

النسبة المئوية للطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحرافين معياريين، أو تزيد عليه بمقدار لا يزيد على ثلاثة انحرافات معيارية هي:

$\frac{1}{2}\left(95\mathrm{\%}\right)+\frac{1}{2}\left(99.7\mathrm{\%}\right)=97.35\mathrm{\%}$

إذا كان: $\mathit{X}\mathbf{~}\mathit{N}\mathbf{(}\mathbf{50}\mathbf{,}{\mathbf{4}}^{\mathbf{2}}\mathbf{)}$، فأجد كلاً من الاحتمالات الآتية باستعمال القاعدة التجريبية:

$P(X<50)$ (5)

$P(X<50)=0.5$

$P(46<X<54)$ (6)

$P(46<X<54)=P(\mu -\sigma <X<\mu +\sigma )=0.68$

$P(42<X<62)$ (7)

$\begin{array}{rl}P(42<X<62)& =P(\mu -2\sigma <X<\mu +3\sigma )\\ & =\frac{1}{2}\left(0.95\right)+\frac{1}{2}\left(0.997\right)=0.9735\end{array}$

صناعة: يمكن نمذجة أطوال أقطار مسامير ينتجها مصنع بمنحنى التوزيع الطبيعي المبين في الشكل المجاور:

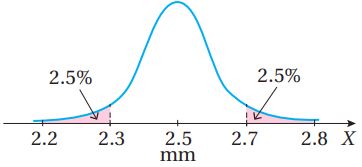
(8) أجد الوسط الحسابي والانحراف المعياري لأطوال أقطار المسامير.

$\begin{array}{rl}& \mu =2.5\mathrm{mm}\\ & 2.7=\mu +2\sigma \Rightarrow 2.7=2.5+2\sigma \Rightarrow \sigma =0.1\mathrm{mm}\end{array}$

(9) أجد النسبة المئوية للمسامير التي يزيد طول قطر كل منها على الوسط الحسابي بما لا يزيد على انحرافين معياريين.

النسبة المئوية للمسامير التي يزيد طول قطر كل منها على الوسط الحسابي بما لا يزيد على انحرافين معياريين هي:

$\frac{1}{2}\left(95\mathrm{\%}\right)=47.5\mathrm{\%}$

(10) أفاع: يدل المتغير العشوائي $X~N(100,{\sigma }^2)$ على أطوال الأفاعي (بالسنتيمتر) في أحد مجتمعاتها. إذا كانت أطوال %68 منها تتراوح بين 93cm و107cm، فأجد ${\sigma }^2$.

نعلم أن %68 تقريباً من البيانات في التوزيع الطبيعي تقع بين $\mu +\sigma ,\mu -\sigma$، فإذن:

$107=\mu +\sigma \Rightarrow 107=100+\sigma \Rightarrow \sigma =7\Rightarrow {\sigma }^2=49$ 

أجد كلاً مما يأتي، مستعملاً جدول التوزيع الطبيعي المعياري:

$P(Z<0.43)$ (11)

$P(Z<0.43)=0.6664$

$P(Z>1.08)$ (12)

$P(Z>1.08)=1-P(Z<1.08)=1-0.8599=0.1401$

$P(Z<-2.03)$ (13)

$P(Z<-2.03)=1-P(Z<2.03)=1-0.9788=0.0212$

$P(Z>2.2)$ (14)

$P(Z>2.2)=1-P(Z<2.2)=1-0.9861=0.0139$

$P(-0.72<Z<0.72)$ (15)

$\begin{array}{rl}P(-0.72<Z<0.72)& =P(Z<0.72)-P(Z<-0.72)\\ =& P(Z<0.72)-(1-P(Z<0.72\left)\right)\\ =& 2P(Z<0.72)-1\\ =& 2\left(0.7642\right)-1=0.5284\end{array}$

$P(1.5<Z<2.5)$ (16)

$\begin{array}{rl}P(1.5<Z<2.5)& =P(Z<2.5)-P(Z<1.5)\\ & =0.9938-0.9332=0.0606\end{array}$

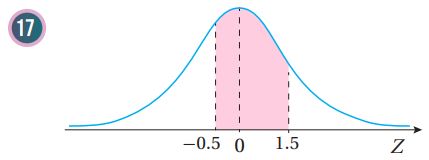
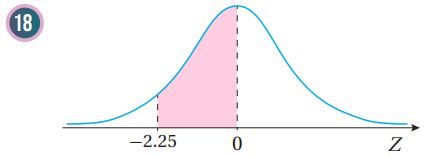
أجد مساحة المنطقة المظللة أسفل منحنى التوزيع الطبيعي المعياري في كل مما يأتي:

$\begin{array}{rl}P(-0.5<Z<1.5)=& P(Z<1.5)-P(Z<-0.5)\\ & =P(Z<1.5)-(1-P(Z<0.5\left)\right)\\ & =P(Z<1.5)+P(Z<0.5)-1\\ & =0.9332+0.6915-1=0.6247\end{array}$

$\begin{array}{rl}P(-2.25<Z<0)& =P(Z<0)-P(Z<-2.25)\\ & =P(Z<0)-(1-P(Z<2.25\left)\right)\\ & =P(Z<0)+P(Z<2.25)-1\\ & =0.5+0.9878-1=0.4878\end{array}$

أجد القيمة المعيارية z التي تحقق كل احتمال مما يأتي:

$P(Z<z)=0.7642$ (19)

الاحتمال المعطى (0.7642) يمثل المساحة التي تقع يسار القيمة z وهو أكبر من 0.5، إذن: z موجبة

$\Rightarrow z=0.72$

$P(Z>z)=0.372$ (20)

الاحتمال المعطى (0.372) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$\Rightarrow P(z<z)=1-0.372=0.628\Rightarrow z=0.33$

$P(Z>z)=0.8531$ (21)

الاحتمال المعطى (8531 .0) يمثل المساحة التي تقع يمين القيمة z و هو أكبر من 0.5، إذن: z سالبة

$\Rightarrow 0.8531=P(Z>-z)=P(Z<z)\Rightarrow z=1.05$

إذن، قيمة z التي تحقق الاحتمال $P(Z>z)=0.8531$ هي 1.05-

إذا كان: $\mathit{X}\mathbf{~}\mathit{N}\mathbf{(}\mathbf{-}\mathbf{3}\mathbf{,}\mathbf{25}\mathbf{)}$، فأجد كل احتمال مما يأتي، مستعملاً جدول التوزيع الطبيعي المعياري:

$P(X<2)$ (22)

$P(X<2)=P(Z<\frac{2+3}{5})=P(Z<1)=0.8413$

$P(X>4.5)$ (23)

$\begin{array}{rl}P(X>4.5)=P(Z>\frac{4.5+3}{5})=P(Z>1.5)& =1-P(Z<1.5)\\ & =1-0.9332=0.0668\end{array}$

$P(-5<X<-3)$ (24)

$\begin{array}{rl}P(-5<X<-3)=& P(\frac{-5+3}{5}<Z<\frac{-3+3}{5})=P(-0.4<Z<0)\\ & =P(Z<0)-P(Z<-0.4)\\ & =P(Z<0)-(1-P(Z<0.4\left)\right)\\ & =P(Z<0)+P(Z<0.4)-1\\ & =0.5+0.6554-1=0.1554\end{array}$

إذا كان X متغيراً عشوائياً طبيعياً، وسطه الحسابي 30، وانحرافه المعياري 10، فأجد قيمة x التي تحقق الاحتمال المعطى في كل مما يأتي:

$\mathrm{P}(X<x)=0.99$ (25)

$P(X<x)=0.99\Rightarrow P(Z<Z)=0.99$

الاحتمال المعطى (0.99) يمثل المساحة التي تقع يسار القيمة z وهو أكبر من 0.5، إذن: z موجبة

$\begin{array}{rl}& z=2.33\\ & \frac{x-30}{10}=2.33\Rightarrow x=53.3\end{array}$

$P(X>x)=0.1949$ (26)

$P(X>x)=P(Z>z)=0.1949$

الاحتمال المعطى (0.1949) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$\begin{array}{rl}& \Rightarrow P(Z<z)=1-0.1949=0.8051\\ & \Rightarrow z=0.86\\ & \Rightarrow \frac{x-30}{10}=0.86\Rightarrow x=38.6\end{array}$

$P(X<x)=0.35$ (27)

$P(X<x)=0.35\Rightarrow P(Z<z)=0.35$

الاحتمال المعطى (0.35) يمثل المساحة التي تقع يسار القيمة z وهو أقل من 0.5، إذن: z سالبة

$\begin{array}{rl}& \Rightarrow P(Z<-z)=P(Z>z)=1-P(Z<z)=0.35\\ & \Rightarrow P(Z<z)=0.65\Rightarrow z=0.39\end{array}$

إذن، قيمة z التي تحقق الاحتمال $P(Z<z)=0.35$ هي 0.39-

$\Rightarrow \frac{x-30}{10}=-0.39\Rightarrow x=26.1$

$P(X>x)=0.05$ (28)

$P(X>x)=0.05\Rightarrow P(Z>z)=0.05$

الاحتمال المعطى (0.05) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$\begin{array}{rl}& \Rightarrow P(Z<z)=1-0.05=0.95\Rightarrow z=1.64\\ & \Rightarrow \frac{x-30}{10}=1.64\Rightarrow x=46.4\end{array}$

رياضة: تتبع أطوال لاعبي كرة السلة توزيعاً طبيعياً، وسطه الحسابي 185cm، وانحرافه المعياري 5cm. إذا اختير لاعب عشوائياً، فأجد كلاً مما يأتي:

(29) احتمال أن يزيد طول اللاعب على  175cm.

$P(X>175)=P(Z>\frac{175-185}{5})=P(Z>-2)=P(Z<2)=0.9772$

(30) احتمال أن يتراوح طول اللاعب بين 180cm و190cm.

$\begin{array}{rl}& P(180<X<190)=P(\frac{180-185}{5}<Z<\frac{190-185}{5})=P(-1<Z<1)\\ & =P(Z<1)-P(Z<-1)=P(Z<1)-(1-P(Z<1\left)\right)\\ & =2P(Z<1)-1=2\left(0.8413\right)-1=0.6826\end{array}$

ملحوظة: يمكن حل هذا السؤال بالاستناد إلى القاعدة التجريبية بدلاً من استخدام الجدول، ويكون الاحتمال 0.68 تقريباً.

(31) العدد التقريبي للاعبين الذين تزيد أطوالهم على 195cm من بين 2000 لاعب.

$\begin{array}{rl}P(X>195)=P(Z>\frac{195-185}{5})=P(Z>2)& =1-P(Z<2)\\ & =1-0.9772=0.0228\end{array}$

إذا كان عدد اللاعبين الذين تزيد أطوالهم على 195cm هو N، فإن:

$N=2000\times 0.0228=45.6\approx 46$

(32) في دراسة عن أشجار الكينا في إحدى الغابات، تبين أن الوسط الحسابي لأطوال هذه الأشجار هو 6m، وأن الانحراف المعياري هو 2m. إذا كانت أطوال الأشجار تتبع توزيعاً طبيعياً، فأجد احتمال أن يكون طول شجرة اختيرت عشوائياً أكثر من 9 أمتار.

$\begin{array}{rl}P(X>9)=P(Z>\frac{9-6}{2})=P(Z>1.5)& =1-P(Z<1.5)\\ & =1-0.9332=0.0668\end{array}$

تعبئة: يعبئ مصنع حبوب القهوة في أوعية من الكرتون. إذا كانت كتل الأوعية تتبع توزيعاً طبيعياً، وسطه الحسابي 232g، وانحرافه المعياري 5g، وكان المتغير العشوائي X يدل على كتلة الوعاء المختار عشوائياً، فأجد كلاً مما يأتي:

(33) $P(X<224)$.

$\begin{array}{rl}P(X<224)=P(Z<\frac{224-232}{5})=P(Z<-1.6)& =1-P(Z<1.6)\\ & =1-0.9452=0.0548\end{array}$

(34) قيمة x، حيث: $P(232<X<x)=0.2$.

$\begin{array}{rl}& P(232<X<x)=P(\frac{232-232}{5}<Z<z)=P(0<Z<z)\\ & \Rightarrow P(Z<z)-P(Z<0)=0.2\\ & \Rightarrow P(Z<z)-0.5=0.2\\ & \Rightarrow P(Z<z)=0.7\end{array}$

الاحتمال المعطى (0.7) يمثل المساحة التي تقع يسار القيمة z وهو أكبر من 0.5، إذن: z موجبة

$\Rightarrow z=0.52\Rightarrow \frac{x-232}{5}=0.52\Rightarrow x=234.6\mathrm{g}$

(35) صناعة: يمثل $X~N(\mu ,169)$ المتغير العشوائي الطبيعي لطول قطر كل من إطارات دراجات هوائية (بالمليمتر) ينتجها أحد المصانع. إذا زاد طول قطر %11 منها على 47cm، فأجد الوسـط الحسابي لأطوال أقطار الإطارات التي ينتجها المصنع.

$P(X>47)=0.11\Rightarrow P(Z>\frac{47-\mu }{13})=0.11$

نفرض $\frac{47-\mu }{13}=z$، أن فيكون: $P(Z>z)=0.11$

الاحتمال المعطى (0.11) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$\begin{array}{rl}& \Rightarrow P(Z<z)=1-P(Z>z)=1-0.11=0.89\\ & \Rightarrow z=1.23\Rightarrow \frac{47-\mu }{13}=1.23\Rightarrow \mu =31.01\end{array}$

(36) اختبارات: تتبع العلامات في أحد الاختبارات توزيعاً طبيعياً، وسطه الحسابي 43. إذا كان X هو المتغير العشوائي للعلامات، فأجد قيمة الانحراف المعياري، علماً بأن احتمال ظهور علامة أعلى من 48 هو 0.2

$P(x>48)=0.2\Rightarrow P(Z>\frac{48-43}{\sigma })=P(Z>\frac{5}{\sigma })=0.2$

نفرض $\frac{5}{\sigma }=Z$، أن فيكون: $P(Z>z)=0.2$

الاحتمال المعطى (0.2) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$\begin{array}{rl}& \Rightarrow P(Z<z)=1-P(Z>z)=1-0.2=0.8\\ & \Rightarrow z=0.84⟹\frac{5}{\sigma }=0.84⟹\sigma =\frac{5}{0.84}\approx 5.95\end{array}$

(37) إذا كان: $X~N(\mu ,{\mu }^2)$، وكانت قيمة z المعيارية المقابلة لقيمة 1=x هي 2=z، فأجد قيمة $\mu$.

$z=\frac{x-\mu }{\sigma }\Rightarrow 2=\frac{1-\mu }{\mu }\Rightarrow 2\mu =1-\mu \Rightarrow \mu =\frac{1}{3}$

(38) إذا كان $X~N(\mu ,{\sigma }^2)$ يمثل توزيعاً طبيعياً، وكانت قيمة z المعيارية المقابلة لقيمة 10=x هي 1=z، وكانت قيمة z المقابلة لقيمة 4=x هي 2-، فأجد قيمة كل من $\mu ,\sigma$.

$\begin{array}{rl}& 1=\frac{10-\mu }{\sigma }\Rightarrow \sigma =10-\mu \dots \dots \dots \dots \dots \left(1\right)\\ & -2=\frac{4-\mu }{\sigma }\Rightarrow -2\sigma =4-\mu \dots \dots \dots \dots \left(2\right)\\ & \text{(1)}-\left(2\right):3\sigma =6\Rightarrow \sigma =2,\mu =8\end{array}$

(39) في دراسة لإدارة السير، تبين أن سرعة السيارات على أحد الطرق تتبع توزيعاً طبيعياً، وسطه الحسابي 90km/h، وانحرافه المعياري 5km/h. إذا كانت السرعة القصوى المحددة على هذا الطريق هي 100km/h، وكان العدد الكلي للسيارات التي تسير على هذا الطريق في أحد الأيام هو 1000 سيارة، فأجد العدد التقريبي للسيارات التي ستتجاوز السرعة المحددة على الطريق في هذا اليوم.

$\begin{array}{rl}P(X>100)=P(Z>\frac{100-90}{5})=P(Z>2)& =1-P(Z<2)\\ & =1-0.9772=0.0228\end{array}$

إذا كان عدد السيارات التي ستتجاوز السرعة المحددة هو N، فإن:

$N=1000\left(0.0228\right)=22.8\approx 23$

(40) يمكن نمذجة كتل البيض في إحدى المزارع بتوزيع طبيعي، وسطه الحسابي 60g، وانحرافه المعياري 4g. أجد عدد البيض صغير الحجم من بين 5000 بيضة في المزرعة، علماً بأن كتلة البيضة الصغيرة لا تزيد على 55 غراماً.

$\begin{array}{rl}P(X\le 55)=P(Z\le \frac{55-60}{4})& =P(Z\le -1.25)\\ & =P(Z>1.25)\\ & =1-P(Z<1.25)\\ & =1-0.8944=0.1056\end{array}$

إذا كان عدد البيض صغير الحجم من بين 5000 هو N، فإن:

$N=5000\left(0.1056\right)=528$