اختبار نهاية الوحدة
التكامل
أختار رمز الإجابة الصحيحة في كل مما يأتي:
(1) قيمة هي:
(a
(b
(c
(d
(2) إذا كان: فإن قيمة الثابت k:
1 (a
2 (b
3 (c
4 (d
(3) قيمة: هي:
(a
(b
(c
(d
(4) قيمة: هي:
(a
(b
(c
(d
(5) قيمة: هي:
2- (a
(b
(c
2 (d
(6) التكامل المحدود الذي يمكن عن طريقه إيجاد المساحة بين منحنى الاقتران: والمحور x هو:
(a
(b
(c
(d
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الآتية:
هذه الإحداثيات تمثل حدود التكامل.
نختار عدداً ضمن الفترة [0,4]، وليكن 1 ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض موجب، إذن منحنى الاقتران يقع فوق المحور x في الفترة [0,4]
والتكامل المحدود الذي يمكن عن طريقه إيجاد المساحة المطلوبة هو
أجد كلاً من التكاملات الآتية:
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24) إذا كان ميل المماس لمنحنى العلاقة y هو: فأجد قاعدة العلاقة، علماً بان منحناها يمر بالنقطة (0,3).
منحنى الاقتران يمر بالنقطة (0,3) إذن:
(25) الإيراد الحدي: يمثل الاقتران: الإيراد الحدي (بالدينار) لكل قطعة تباع في إحدى الشركات، حيث x عدد القطع المبيعة، و(R(x إيراد بيع x قطعة بالدينار. أجد اقتران الإيراد R(x)، علماً بأن R(20)=30000.
بما أن R(20)=30000 إذن:
(26) يتحرك جسيم من السكون، ويعطى تسارعه بالاقتران: ، حيث t الزمن بالثواني، وa تسارعه بالمتر لكل ثانية تربيع. أجد سرعة الجسيم بعد t ثانية من بدء الحركة.
إذا كان ، فأجد كلاً مما يأتي:
(27)
(28)
(29)
أجد قيمة كل من التكاملات الآتية:
(30)
(31)
(32)
أعيد تعريف اقتران القيمة المطلقة:
بما أن الاقتران تشعب عند 3، فإنني أجزئ التكامل عنده:
(33)
(34)
(35)
(36)
(37)
(38) إذا كان: ، فأجد قيمة: .
بما أن الاقتران تشعب عند 0، فإنني أجزئ التكامل عنده:
(39) يتحرك جسم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: ، حيث t الزمن بالثواني، وv سرعته المتجهة بالمتر لكل ثانية، إذا الجسيم حركته من نقطة الأصل، فأجد موقعه بعد 3 ثوان من بدء الحركة.
بما أن الجسيم بدأ حركته من نقطة الأصل، إذن s(0)=0:
موقع الجسم بعد 3 ثوان من الحركة هو:
في كل مما يأتي المشتقة الأولى للاقتران (f(x، ونقطة يمر بها منحنى (y=f(x. أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران (f(x:
(40)
بما أن منحنى الاقتران يمر بالنقطة (0,6) إذن:
(41)
بما أن منحنى الاقتران يمر بالنقطة (1,400) إذن:
(42)
بما أن منحنى الاقتران يمر بالنقطة (1,1) إذن:
(43)
بما أن منحنى الاقتران يمر بالنقطة (1-,0) إذن:
(44)
بما أن منحنى الاقتران يمر بالنقطة (2,10) إذن:
(45) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: ، والمحور x، والمستقيمين: x=1,x=-2
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
نختار عدداً ضمن الفترة [2,1-]، وليكن 1.5- ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض موجب، إذن منحنى الاقتران يقع فوق المحور x في الفترة [1-,2-]
نختار عددا ضمن الفترة [1,1-]، وليكن 0 ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض سالب، إذن منحنى الاقتران يقع تحت المحور x في الفترة [1,1-]
العدد 2 خارج الفترة المطلوبة بالسؤال، إذن نهمله
إذن، المساحة هي: وحدة مربعة.
(46) طب: يمثل الاقتران (1)C تركيز دواء في الدم بعد t ساعة من حقنه في جسم مريض، حيث C مقيسة بالمليغرام لكل سنتيمتر مكعب . إذا كان تركيز الدواء فـي دم المريض يتغير بمعدل ، فأجد مقدار التغير في تركيز الدواء بالدم خلال الساعات الثماني الأولى التي تلت حقنه في جسم المريض.
أولاً نجد قاعدة الاقتران:
بما أن مقدار تركيز الدواء في الدم في البداية هي 0 مليغرام، إذن 0=(0)C ومنه:
مقدار التغير في تركيز الدواء في الجسم خلال الساعات الثماني الأولى من حقنه هو
(47) أجد مساحة المنطقة المحصورة بين منحنى الاقتران ، والمحور x.
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
هذه الإحداثيات تمثل حدود التكامل.
نختار عدداً ضمن الفترة [0,1]، وليكن ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض سالب، إذن منحنى الاقتران يقع تحت المحور x في الفترة [0,1]
إذن، المساحة هي: وحدة مربعة.
أجد مساحة المنطقة المظللة في كل من التمثيلات البيانية الآتية:
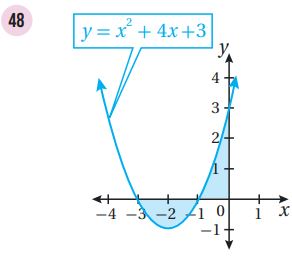
إذن، المساحة هي: وحدة مربعة.

إذن، المساحة هي: وحدة مربعة.

إذن، المساحة هي: وحدة مربعة.

إذن، المساحة هي: وحدة مربعة.




النقاشات