قانون جاي - لوساك

Gay-Lussac’s Law

وجد العالم جاي - لوساك أن العلاقة بين ضغط الغاز ودرجة حرارته علاقة طردية، ووضع قانوناً عُرف باسمه.

نص قانون جاي - لوساك

"ضغط كمية محددة من الغاز المحصور يتناسب طردياً مع درجة حرارته المطلقة عند ثبات حجمه".

تفسير قانون جاي - لوساك استناداً إلى افتراضات نظرية الحركة الجزيئية:

عند زيادة درجة الحرارة لجزيئات الغاز المحصور يزداد متوسط الطاقة الحركية للجزيئات، ومن ثم تزداد سرعتها، وتزداد عدد التصادمات مع جدران الوعاء، ولأن حجم الغاز ثابت فإن ضغطه يزداد.

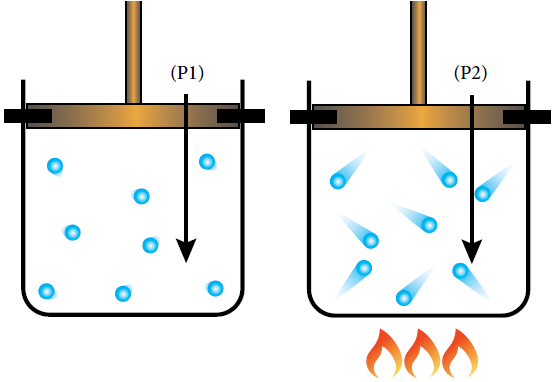
اشتقاق القانون

يُعبّر عن قانون جاي لوساك رياضيّاً على النحو الآتي:

عند ثبات الحجم (V) فإن ضغط الغاز (P) يتناسب طردياً مع درجة حرارته المطلقة (T):

P $\alpha$ V

وبتحويل إشارة التناسب إلى إشارة مساواة نضرب في ثابت (k):

P = k V

وبترتيب حدود العلاقة:

k = $\frac{\mathrm{P}}{\mathrm{V}}$

فلو كان لدينا ظرفان مختلفان للغاز، يكون:

k = $\frac{{\mathrm{P}}_1}{{\mathrm{V}}_1}$

k = $\frac{{\mathrm{P}}_2}{{\mathrm{V}}_2}$

وبمساواة الحدين، نحصل على قانون جاي – لوساك:

$\frac{{\mathrm{P}}_1}{{\mathrm{V}}_1}$ = $\frac{{\mathrm{P}}_2}{{\mathrm{V}}_2}$

أمثلة محلولة

مثال (1):

غاز ضغطه 1.5 atmعند درجة 27⁰C، كم يصبح ضغطه عند درجة 47⁰C عند  ثبوت حجمه.   

تحليل السؤال (المعطيات)

T₁ = 27 + 273 = 300 K

T₂ = 47 + 273 = 320 K

P₁ = 1.5 atm

P₂ = ??

الحل:

$\frac{{\mathrm{P}}_1}{{\mathrm{T}}_1}$ = $\frac{{\mathrm{P}}_2}{{\mathrm{T}}_2}$

$\frac{1.5}{300}$ = $\frac{{\mathrm{P}}_2}{320}$

P₂ = 1.6 atm

مثال (2):

تنفجر علب بخاخات الشعر إذا زاد الضغط فيها عن 3 atm. فإذا كان الضغط داخل إحدى العلب 2.4 atm عند درجة 27⁰C ، فما مقدار الدرجة الحرارية السليسيوسية التي يمكن للعلبة أن تتحمله.

تحليل السؤال (المعطيات)

T₁ = 27 + 273 = 300 K

T₂ = ??

P₁ = 3 atm

P₂ = 2.4 atm

الحل:

$\frac{{\mathrm{P}}_1}{{\mathrm{T}}_1}$ = $\frac{{\mathrm{P}}_2}{{\mathrm{T}}_2}$

$\frac{2.4}{300}$ = $\frac{3}{{\mathrm{T}}_2}$

T₂ = 375 K

درجة الحرارة السليسيوسية = 102⁰C = 375 - 273

أتحقق صفحة (63):

إذا كان ضغط الهواء داخل إطار سيارة 1.85 atm عند 27⁰C ، وبعد قيادتها لمسافة معينة أصبح 2.2 atm . أحسب درجة حرارته، بفرض ثبات حجمه.

تحليل السؤال (المعطيات)

T₁ = 27 + 273 = 300 K

T₂ = ??

P₁ = 1.85 atm

P₂ = 2.2 atm

الحل:

$\frac{{\mathrm{P}}_1}{{\mathrm{T}}_1}$ = $\frac{{\mathrm{P}}_2}{{\mathrm{T}}_2}$

$\frac{1.85}{300}$ = $\frac{2.2}{{\mathrm{T}}_2}$

T₂ = 356.75 K