أسئلة المحتوى وإجاباتها

الكميات القياسية والكميات المتجهة

تجربة استهلالية صفحة (9):

ناتج جمع قوتين عملياً

التحليل والاستنتاج:

1- ماذا تمثل قراءة الميزان الأول في الحالة (أ)؟

تمثل قراءة الميزان الأول في الحالة A وزن الثقل: (W = mg = 0.5 x 10 = 5N).

2- كيف تغيرت قراءة كل من الميزانين في الحالتين (ب) و (ج)؟

الميزان الأول: تناقصت قراءة الميزان إلى النصف في الحالة  B(2.5 N)، ثم ازدادت لتعود إلى قيمتها الأولى في الحالة  C(5 N).

الميزان الثاني: تشابهت قراءة الميزان تشابهاً تاماً مع قراءة الميزان الأول في الحالتين:  B(2.5 N)، و  C(5 N)؛ إذ ازدادت القراءة.

3- أقارن مجموع قراءة الموازين في الحالة (ب) والحالة (ج) بوزن الثقل.

الحالة B : مجموع قراءة الميزان الأول وقراءة الميزان الثاني (2.5 + 2.5 = 5 N) يساوي وزن الثقل 5N .

الحالة C : المجموع المتجهي لقراءة الميزان الأول وقراءة الميزان الثاني (5 + 5 = 5 N) يساوي وزن الثقل 5N .

4- أقوم: أحدد أيهما أؤيد: ادعاء هيا أم ادعاء يمان، ماذا أستنتج؟

صحة ادعاء كل من هيا ويمان تعتمد على مقدار كل من القوتين واتجاهها؛ ففي الحالة C ، حيث الزاوية بين المتجهين 120^o ، يكون ادعاء يمان صحيحاً (5 + 5 = 5 N). وفي الحالة B ، حيث القوتان متوازيتان (الزاوية بينهما  0^o)، يكون ادعاء هيا صحيحاً. نستنتج من ذلك أن ناتج جمع القوى يعتمد على مقادير واتجاهات تلك القوى.

الشكل (1) صفحة (10):

حالة الطقس المتوقعة في العاصمة عمان.

ما الكميات الفيزيائية التي ظهرت في النشرة الجوية؟ هل اختلف وصف كل منها عن غيره؟

الكميات الفيزيائية هي درجة الحرارة، وسرعة الرياح، وقد اختلف وصف كل منها؛ إذ وصفت درجة الحرارة بالمقدار فقط، في حين وصفت سرعة الرياح بالمقدار والاتجاه معاً (اتجاه السهم يمثل اتجاه السرعة).

تمرين صفحة (12):

في أثناء جلوسي في غرفة الصف سقط قلم باتجاه سطح الأرض. أحدد كميتين قياسيتين وكميتين متجهتين لها صلة بذلك.

الكميات القياسية: كتلة القلم، زمن سقوط القلم.

الكميات المتجهة: وزن القلم (قوة جذب الأرض للقلم)، تسارع القلم.

أتحقق صفحة (12):

أقارن بين الكميات المتجهة والكميات القياسية.

الكميات المتجهة: كميات لها مقدار واتجاه، وهي تحدد بالمقدار والاتجاه معاً.

الكميات القياسية: كميات لها مقدار، وليس لها اتجاه، وهي تحدد بالمقدار فقط.

أتحقق صفحة (14):

كيف يمكن تحديد كل من طول السهم واتجاهه عند تمثيل المتجه بيانياً؟

لتحديد طول السهم، يُختار مقياس رسم مناسب، ثم يُحسب طول السهم باستعمال العلاقة الآتية:

طول السهم = مقدار الكمية الفيزيائية × مقياس الرسم

أما اتجاه السهم فهو المتجه نفسه.

تمرين صفحة (14):

تسير سيارة بسرعة v مقدارها 80 km/h ، في اتجاه يصنع زاوية مقدارها 37^o جنوب الشرق. أمثل متجهة السرعة بيانياً.

مقياس الرسم (1 cm : 10 km/h)

طول السهم  في الاتجاه المبين في الشكل الآتي:

أفكر صفحة (14):

استخدم أحمد مقياس الرسم (1 cm : 20 m) لرسم مُتجه يُمثل بُعد المسجد عن منزله كما في الشكل. أحدد بُعد المسجد عن منزل أحمد، مبيناً الاتجاه.

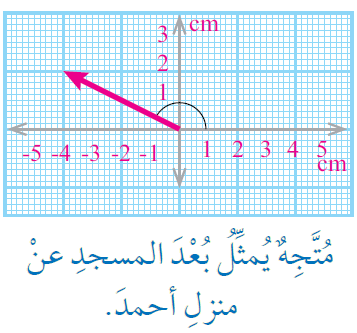
أفكر صفحة (15):

لماذا يكون اتجاه التسارع a دائماً في نفس اتجاه محصلة القوى F$\sum _{}$ ؟

لأن الكتلة m دائماً موجبة، وناتج ضرب كمية متجهة (a) في كمية قياسية موجبة (m) يكون كمية متجهة (m a = F) في اتجاه المتجه نفسه.

أتحقق صفحة (15):

ما المقصود بكل مما يأتي:

• تساوي متجهين؟

متجهان لهما المقدار نفسه، والاتجاه نفسه.

• ضرب متجه في عدد سالب؟

متجه جديد مقداره يساوي مقدار المتجه الأصلي مضروباً في القيمة المطلقة للعدد السالب، واتجاهه عكس اتجاه المتجه الأصلي.

تمرين صفحة (16):

تسير سيارة بتسارع ثابت v مقدارها a = 3 m/s² في اتجاه يصنع زاوية مقدارها 30^o شرق الشمال. أمثل بيانياً.

أ- سالب المتجهه a .

ب- ضرب المتجهه a في العدد (2).

مقياس الرسم (1 cm : 1 m/s²)، إذن، طول السهم الذي يمثل المتجهه a هو 3 cm كما في الشكل.

أ- سالب المتجهه a (-a): هو متجه طوله 3 cm ، بعكس اتجاه a كما في الشكل.

ب- ضرب المتجهه a في العدد (2) (2 a): هو متجه طوله 6 cm ، باتجاه المتجه a .

الشكل (10) صفحة (17):

متجهان بينهما زاوية $\theta$ .

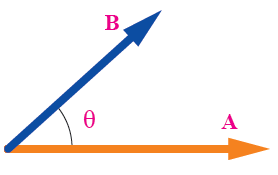
أقارن بين ناتج كل من: A . B ،  B . A

A.B = A B cos $\theta$ 

B.A = B A cos $\theta$

بما أن: $\theta$ A B cos $\theta$ = B A cos

فإن: A.B = B.A

أفكر صفحة (19):

إذا أشارت الأصابع إلى المتجه A ، وأشار الإبهام إلى المتجه B ، فهل تتغير نتيجة الضرب المتجهي؟ أوضّح ذلك.

نعم؛ إذ ينعكس ناتج الضرب المتجهي، أمّا المقدار فلا يتغير. وهذه الحالة تمثل A x  B  .

أتحقق صفحة (19):

ما الفرق بين الضرب المتجهي والضرب القياسي؟

الضرب القياسي: عملية ضرب كمية متجهة في كمية أخرى متجهة أخرى، يكون ناتجها كمية قياسية غير متجهة، لها مقدار فقط على النحو الآتي:

A . B = A B sin $\theta$

الضرب المتجهي: عملية ضرب كمية متجهة في كمية أخرى متجهة، يكون ناتجها كمية متجهة لها مقدار واتجاه.

IA x BI = A B cos $\theta$ 

أما الاتجاه فيحدد بستعمال قاعدة الكف اليمنى.

تمرين صفحة (20):

متجهان: A ، B مقدار كل منهما 20 u (الرمز u يعني وحدة unit).

أجد مقدار الزاوية بين المتجهين في الحالتين الآتيتين:

أ- A . B = 320 u

A . B = A B cos Ɵ 

 320 = 20 x 20 x cos Ɵ

cos Ɵ = 0.8

Ɵ = cos^-1 0.8 = 37^o

ب- IA x BI = 200 u

 IA x BI = A B sin Ɵ

            = 20 x 20 x sin Ɵ 200

sin Ɵ = 0.5

Ɵ = sin^-1 0.5 = 30^o , 150^o