مهارات التفكير العليا

الاقترانات المتشعبة

(12) تبرير: ادعت سارة أنه يمكنها تمثيل الاقتران المتشعب: $f\left(x\right)=\{\begin{array}{ll}x+4& ,x<-2\\ -2x-2& ,x\ge -2\end{array}$ بسهولة، وذلك بتمثيل كلّ من قاعدتيه بيانياً، وافتراض أن مجال كل منهما على حدة هو مجموعة الأعداد الحقيقية كلها، ثم محو أجزاء المنحنى التي تقع خارج المجال المحدد في الاقتران المتشعب كما في الشكل الآتي. هل ادعاء سارة صحيح؟ أبرر إجابتي.

نعم صحيح؛ لأن محو الأجزاء التي لا تقع ضمن المجال المحدد يُبقي تمثيل الاقتران المطلوب، مع مراعاة وضع دائرة مفتوحة أو مغلقة عند أطراف الفترة إن وجدت فجوات أو قفزات في التمثيل البياني.

(13) مسألة مفتوحة: أكتب اقتراناً متشعباً f(x) ، بحيث f(2) = f(3) = 5 , f(-2) = f(-1) = 3 .

إجابة محتملة:

$f\left(x\right)=\{\begin{array}{ll}3,& x<0\\ 5,& x\ge 0\end{array}$

(14) تحدّ: أكتب الاقتران المتشعب: $h\left(x\right)=\{\begin{array}{ll}3& ,x=1\\ 2-x& ,x\ne 1\end{array}$ بيانياً، ثم أحدد مجاله ومداه.

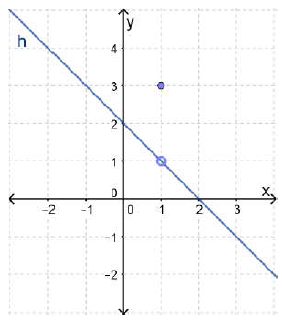
مجال الاقتران h هو جميع قيم x الحقيقية، ومداه هو جميع قيم y الحقيقية ما عدا العدد 1.