أتدرب وأحل المسائل
الاقترانات المثلثية
أجد قيم الاقترانات المثلثية الستة للزاوية Ɵ في كلّ ممّا يأتي:
1)
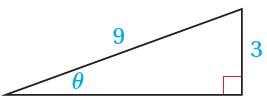
2)

3)

تقع النقطة المعطاة في كلّ مما يأتي على ضلع انتهاء الزاوية Ɵ المرسومة في الوضع القياسي. أجد قيم الاقترانات المثلثية الستة للزاوية Ɵ .
4) (-12, 5)
5) (3, -3)
6) (-2, -5)
7) (3, 7)
أجد قيمة كلّ ممّا يأتي:
8) sec 135o
9)
10)
11)
12)
13) csc (-630o)
14) tan 7π
15)
أجد قيمة كل من الاقترانات المثلثية الخمسة المتبقية للزاوية Ɵ في كلّ ممّا يأتي:
16)
17)
18)
19)
 (20) بكرة: يمثل الاقتران: y = 20 + sin (10t) الارتفاع الرأسي عن سطح الأرض بالسنتيمترات لسِنّ بكرة دراجة هوائية بعد t ثانية من بدء حركة الدارجة. أجد الارتفاع الرأسي لسِنّ البكرة بعد 2.5 ثانية من بدء حركة الدرّاجة.
(20) بكرة: يمثل الاقتران: y = 20 + sin (10t) الارتفاع الرأسي عن سطح الأرض بالسنتيمترات لسِنّ بكرة دراجة هوائية بعد t ثانية من بدء حركة الدارجة. أجد الارتفاع الرأسي لسِنّ البكرة بعد 2.5 ثانية من بدء حركة الدرّاجة.
إذا كان: cos = 0.966 لأقرب ثلاث منازل عشرية فأستعمل هذه الحقيقة لإيجاد قيمة كلّ ممّا يأتي:
21) cos
22) cos
23) cos
24) cos
أجد قيمة كلّ ممّا يأتي:
25)
26)
يبين الشكل المجاور قطاعاً دائرياً، طول نصف قطره r، وطول قوسه 2r . إذا كانت مساحة الجزء المظلل من القطاع 24 cm2 ، فأجد كلاً ممّا يأتي:
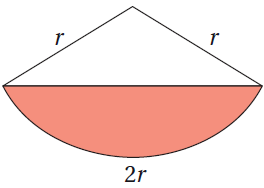
(27) طول نصف قطر القطاع.
نفترض Ɵ زاوية القطاع.
(28) محيط الجزء المظلل.
نفترض طول الضلع الثالث في المثلث الأبيض يساوي h
نجد عن طريق قانون جيب التمام أو بإنزال عمود من رأس المثلث المتطابق الضلعين على القاعدة.
فنجد h = 2r sin 1
محيط الشكل المظلل:
أجد قيمة كلّ ممّا يأتي (إن وجدت):
29)
30) tan-1 (-1)
31)
32) cos-1 (2)



 (20) بكرة: يمثل الاقتران: y = 20 + sin (10t) الارتفاع الرأسي عن سطح الأرض بالسنتيمترات لسِنّ بكرة دراجة هوائية بعد t ثانية من بدء حركة الدارجة. أجد الارتفاع الرأسي لسِنّ البكرة بعد 2.5 ثانية من بدء حركة الدرّاجة.
(20) بكرة: يمثل الاقتران: y = 20 + sin (10t) الارتفاع الرأسي عن سطح الأرض بالسنتيمترات لسِنّ بكرة دراجة هوائية بعد t ثانية من بدء حركة الدارجة. أجد الارتفاع الرأسي لسِنّ البكرة بعد 2.5 ثانية من بدء حركة الدرّاجة.
النقاشات